(Lecture 6) Detecting phase transition in time-varying weighted graphs from partial information

Lecture 6: Detecting phase transition in time-varying weighted graphs from partial information: Forman-Ricci Curvature, phase transition detection algorithms, case studies and applications

---

강의 개요

이번 강의에서는 Forman-Ricci Curvature (FRC)를 중심으로, 시변 네트워크(Time-Varying Networks)에서의 구조적 변화와 상 변화 탐지(Phase Transition Detection)를 다룬다.
FRC의 정의, 계산법, 주요 특성, 그리고 다양한 응용 사례를 상세히 살펴본다.

---

1. Forman-Ricci Curvature (FRC)

• FRC 정의
  FRC는 그래프의 엣지에 곡률 값을 할당하여 구조적 역할과 상호작용 강도를 분석한다.
  엣지 $e = (i, j)$의 FRC는 다음과 같이 계산된다:
  $
  F(e) = w_e \left( \frac{1}{w_i} + \frac{1}{w_j} \right) - \sum_{\text{triangles}} \frac{1}{w_\triangle}
  $
  • $w_e$: 엣지의 가중치.
  • $w_i, w_j$: 노드 $i$와 $j$의 가중치.
  • $w_\triangle$: 삼각형 내부 엣지의 가중치.

• FRC의 특성
  • 계산 효율성: Ollivier-Ricci Curvature(ORC)보다 계산이 간단하며, 대규모 네트워크에서도 적용 가능하다.
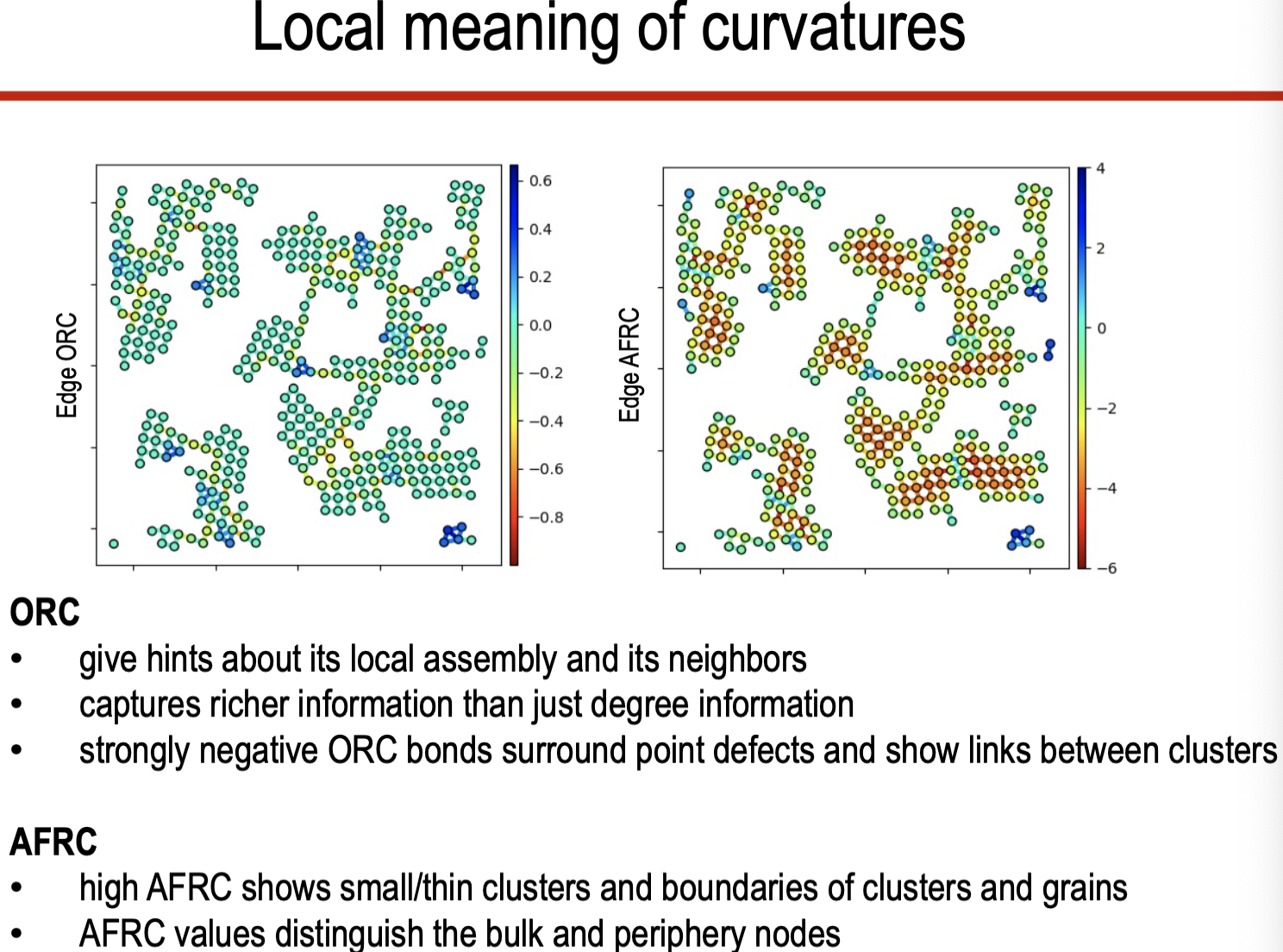
  • 국소적 정보 반영: 엣지와 인접 노드 및 삼각형 간의 관계를 포함한다.
  • 구조적 변화 탐지: 네트워크의 군집성, 다리 역할, 무작위화 정도를 효과적으로 분석한다.

---

2. 시변 네트워크(Time-Varying Networks)

• 정의
  • 시간에 따라 노드와 엣지의 상호작용이 변화하는 네트워크.
  • 이러한 네트워크는 복잡한 동역학적 패턴을 포함하며, 다양한 실제 데이터에 적용된다.
• 적용 사례
  • 사회 네트워크: 사용자 간 관계 변화 분석.
  • 뇌 네트워크: 뇌 활동 변화와 병리학적 변화 추적.
  • 생물학적 네트워크: 단백질 상호작용의 시변 패턴 분석.
  • 나노 물질 네트워크: 자기조립 과정 중 구조적 변화 감지.

Time-Varying Complex Network (TVCNs)

---

3. 상 변화 탐지 (Phase Transition Detection)

• FRC 기반 상 변화 탐지
  • FRC는 네트워크 엔트로피를 계산하여 시변 네트워크의 상 변화 또는 전환점을 탐지한다.
  • 네트워크 엔트로피는 다음과 같이 정의된다:
    $
    \text{FRNE}(t) = -\sum_e F(e) \log F(e)
    $
    여기서 $F(e)$는 엣지 $e$의 Forman-Ricci Curvature이다.

Phase transition prediction for TVCNs

• 랜덤 네트워크 실험
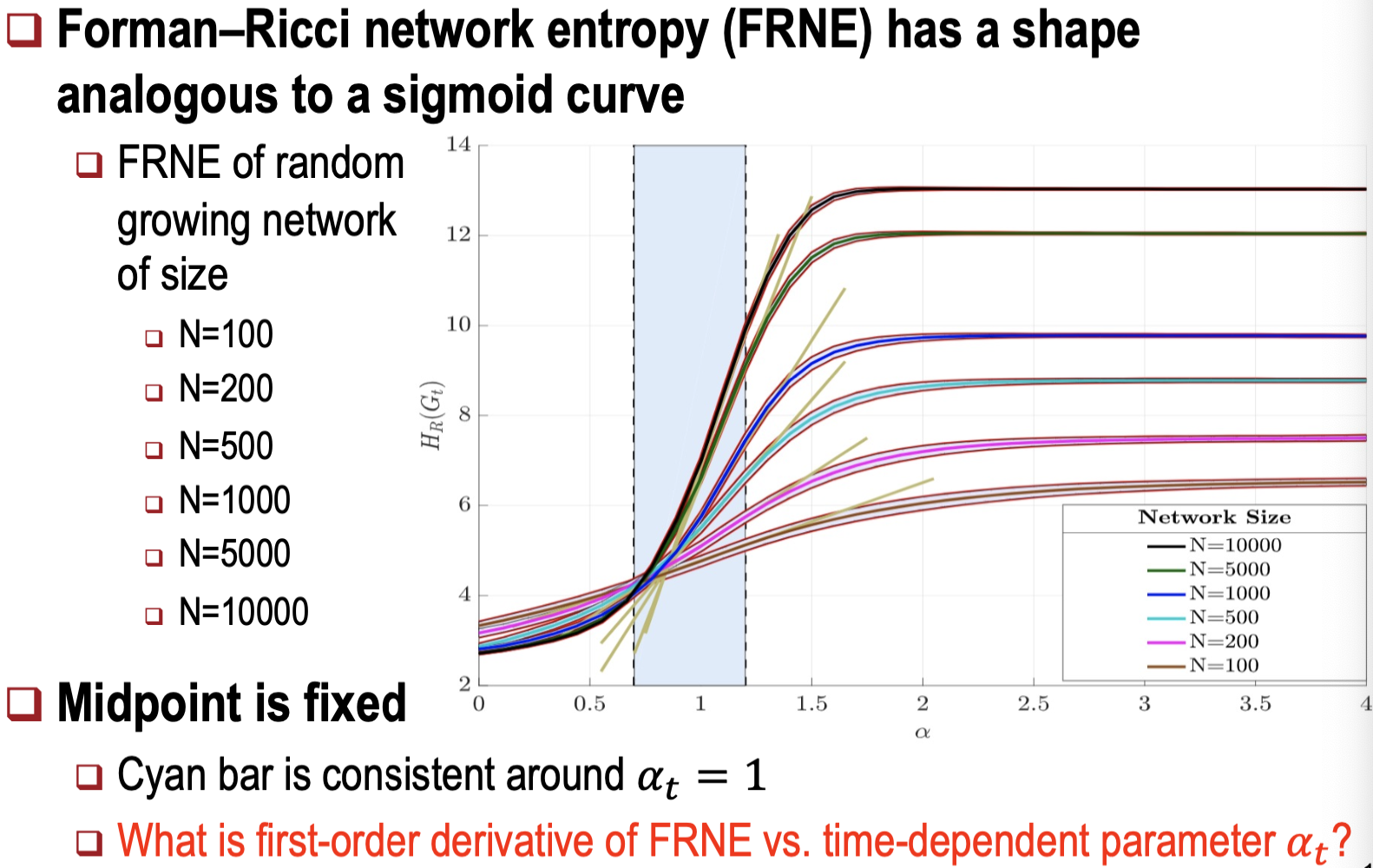
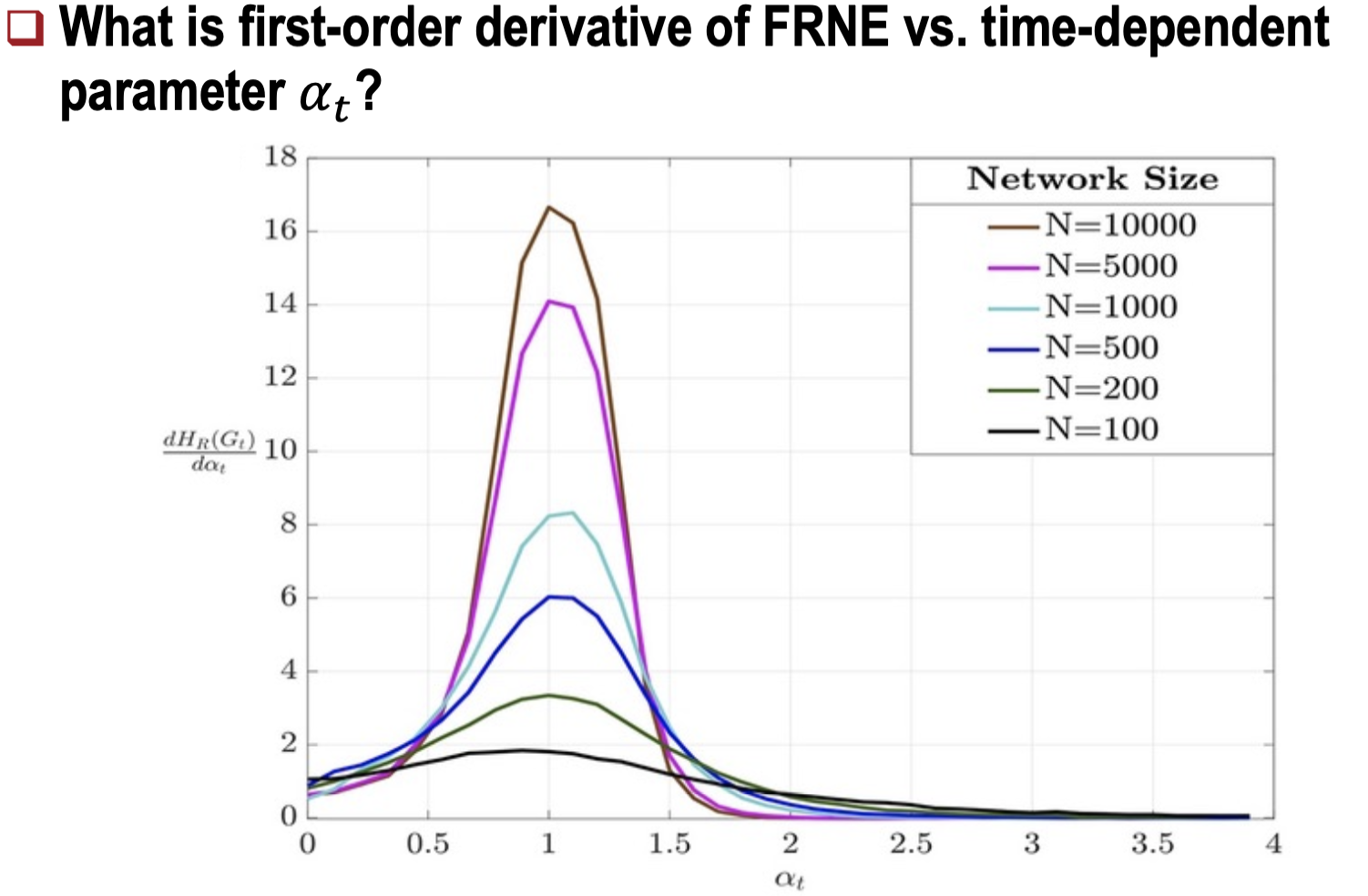
  • Barabási-Albert 모델과 Erdos-Rényi 모델:
    두 모델을 비교한 결과, 엔트로피 변화가 시그모이드 형태를 보이며 상 변화 구간을 나타낸다.
  • 엔트로피 변화는 네트워크 구조의 무작위화 또는 군집화 변화와 일치한다.

Experiments: Random growing networks

---

4. 사례 연구

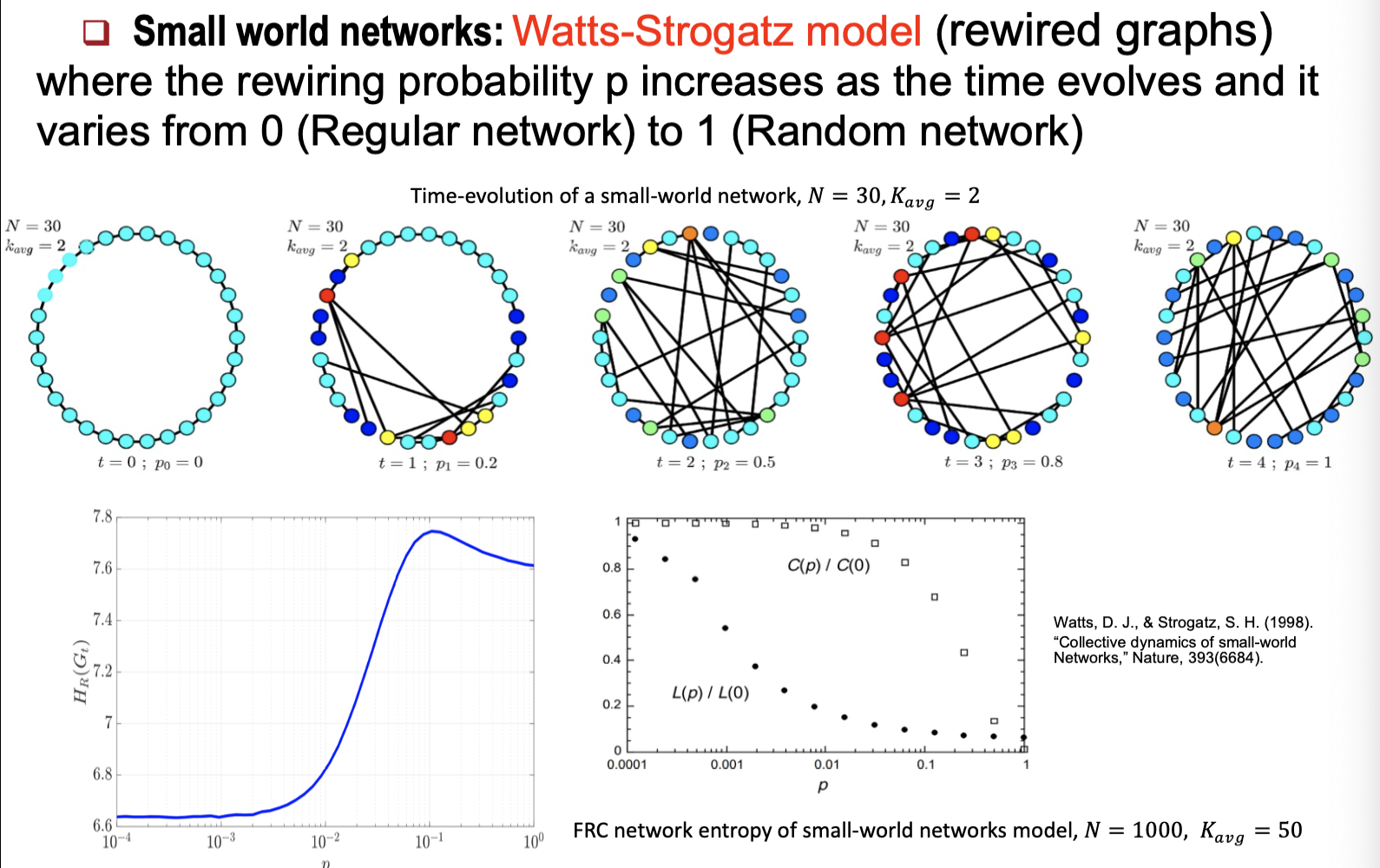
• Small-World Networks
  • Watts-Strogatz 모델:
    재배선 확률 $p$에 따른 네트워크 변화를 분석.
    FRC는 재배선 확률에 따라 군집성의 변화를 효과적으로 설명한다.

Experiments: Small world networks

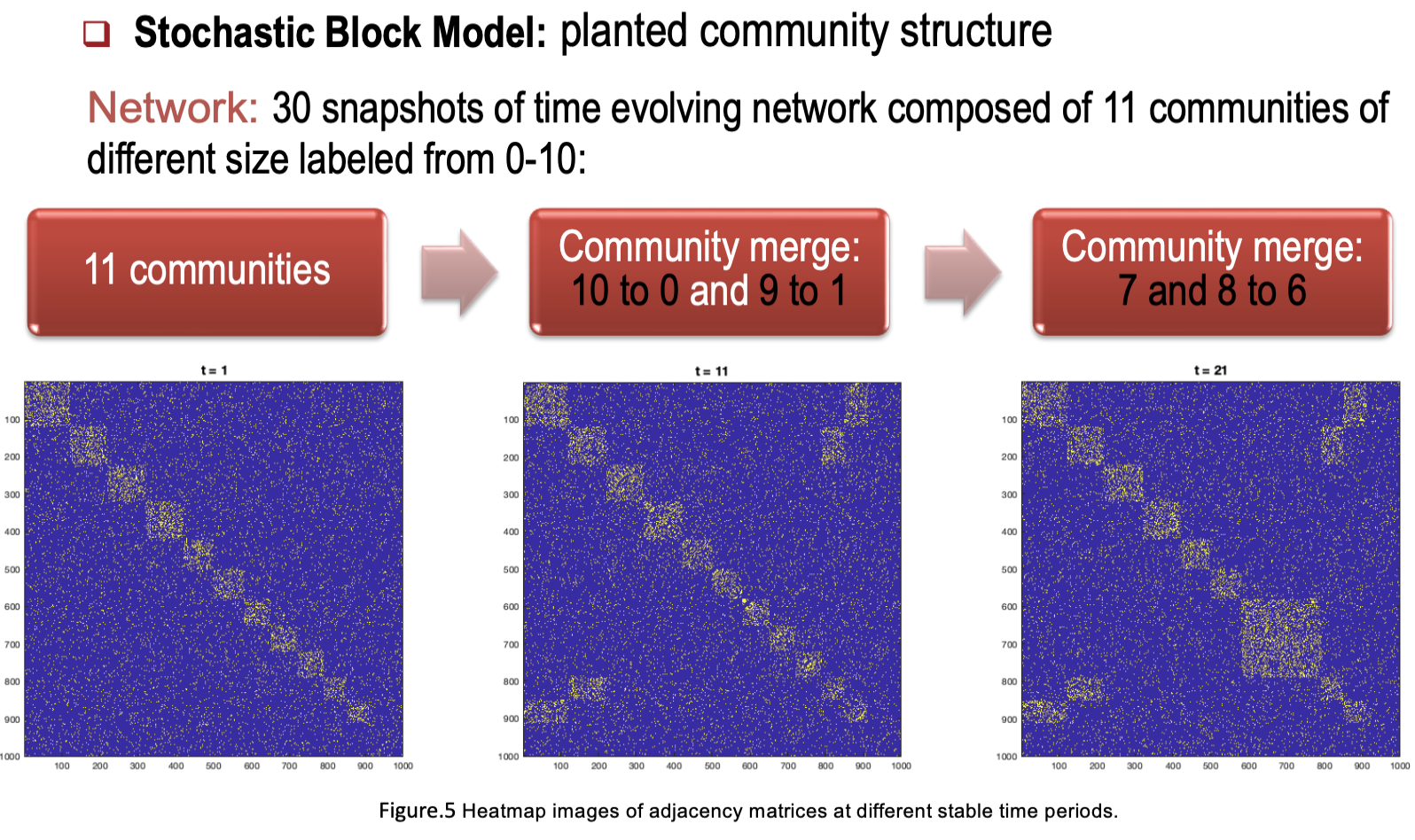
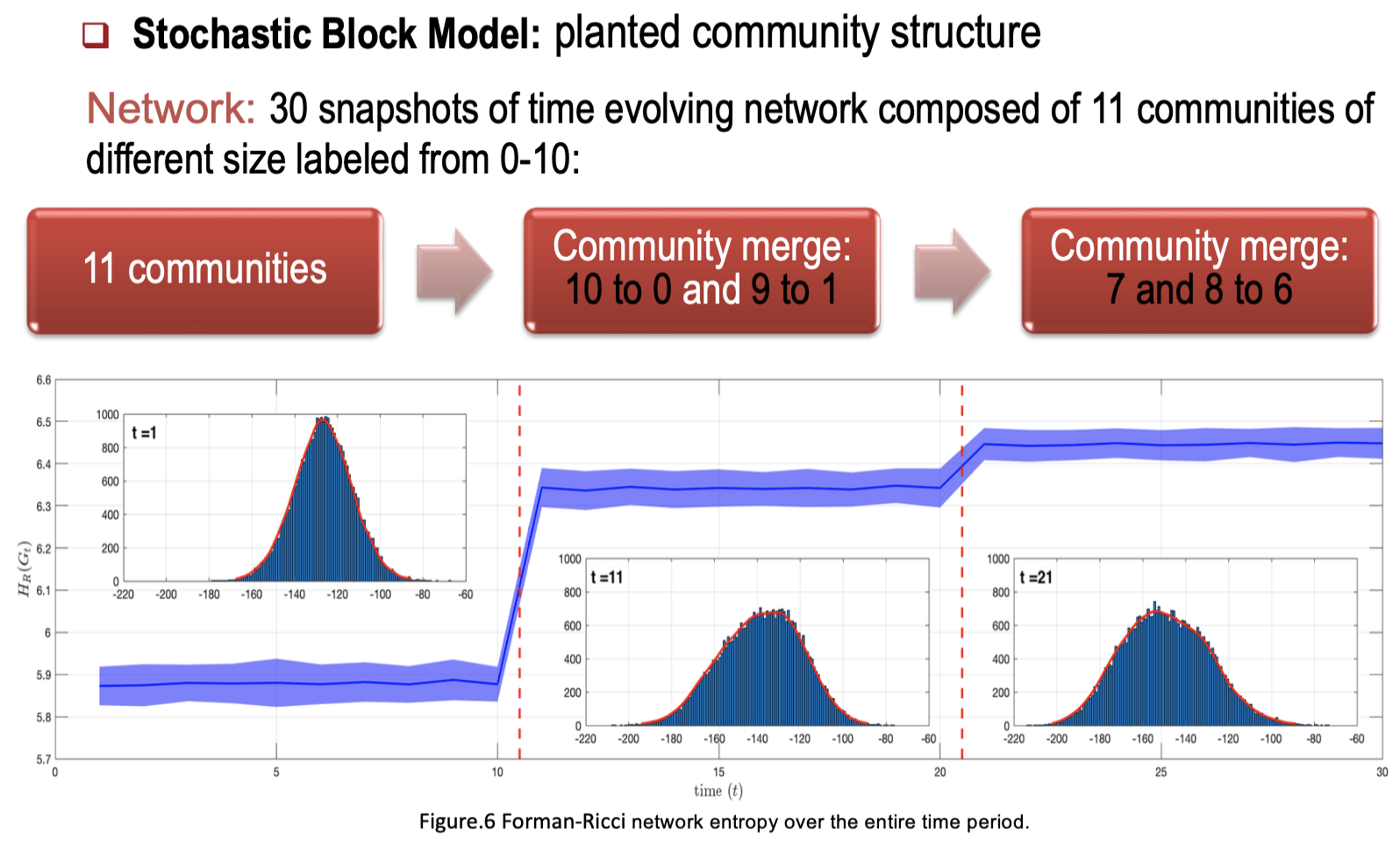
• Stochastic Block Model (SBM)
  • 커뮤니티 병합과 같은 구조적 변화를 FRC 엔트로피로 탐지한다.
  • 커뮤니티 병합 시 FRC 엔트로피가 급격히 변화한다.

Experiments: SBM

• 실세계 데이터
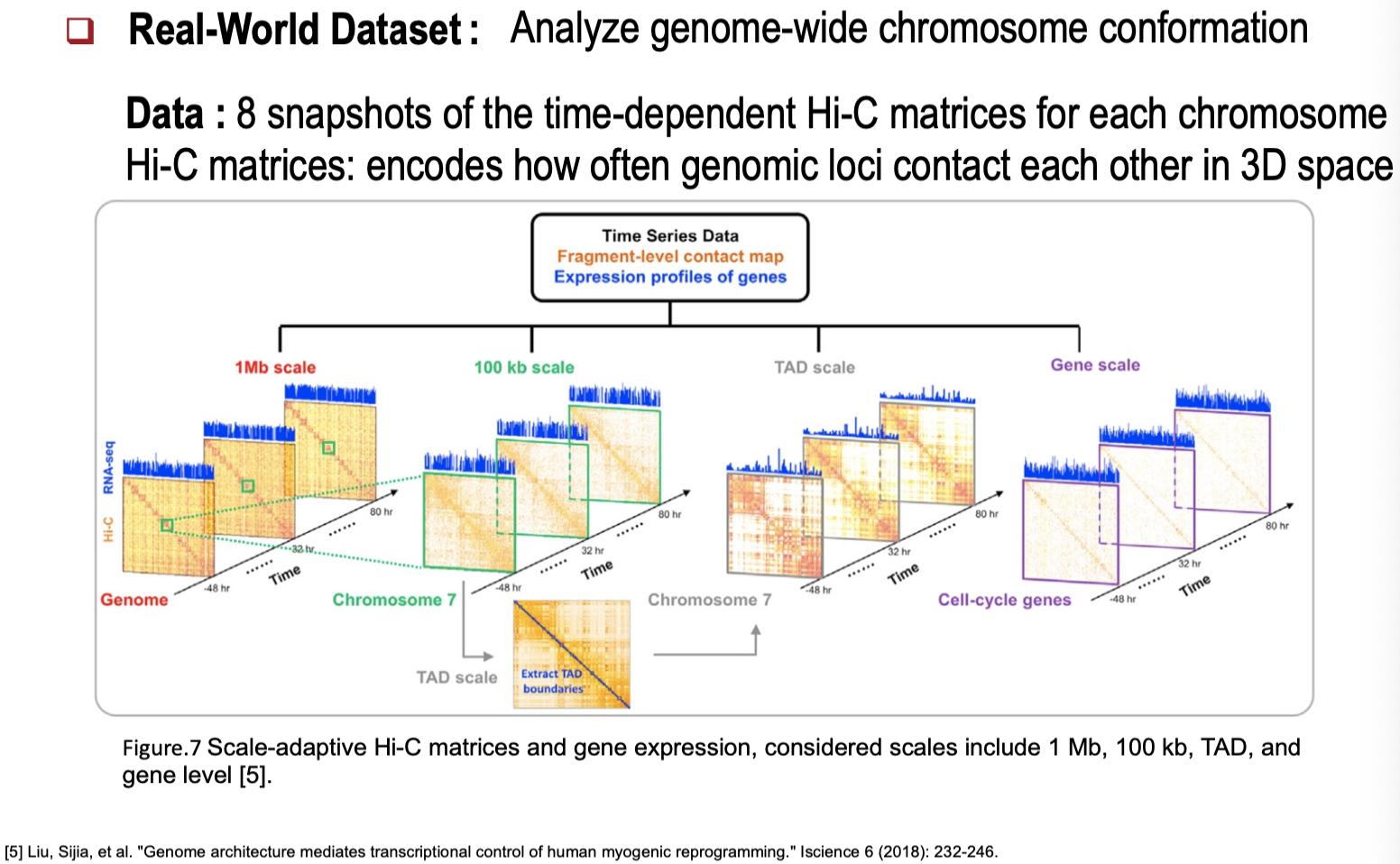
  • Hi-C 데이터:
    인간 게놈의 3차원 구조를 FRC로 분석하여 구조적 재구성을 탐지.

 

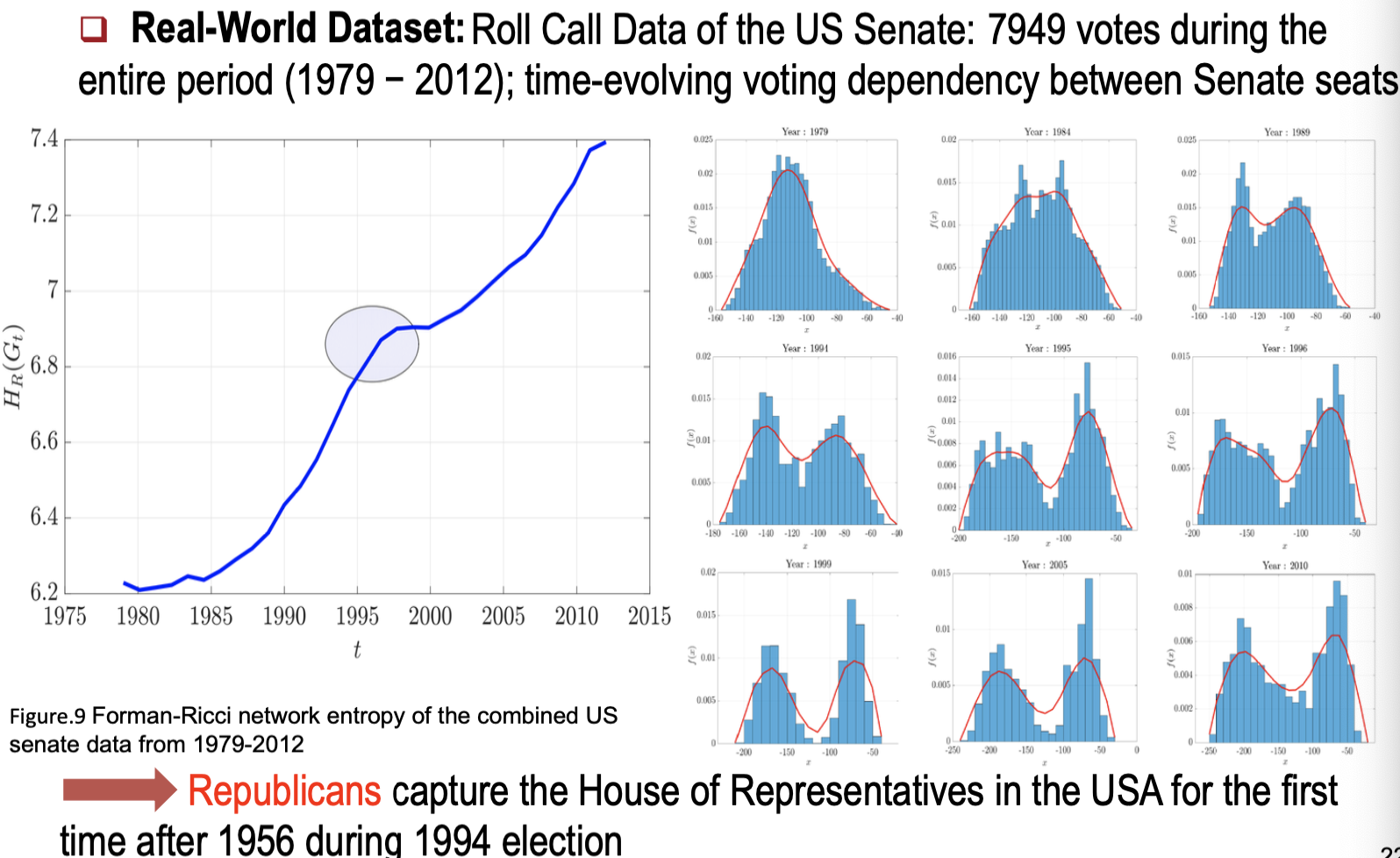
• 미국 상원 투표 데이터:
  1979-2012년 동안 의회 상호작용의 변화 분석.
  FRC는 정치적 정렬과 변화 시기를 효과적으로 나타낸다.

---

5. FRC의 응용 분야

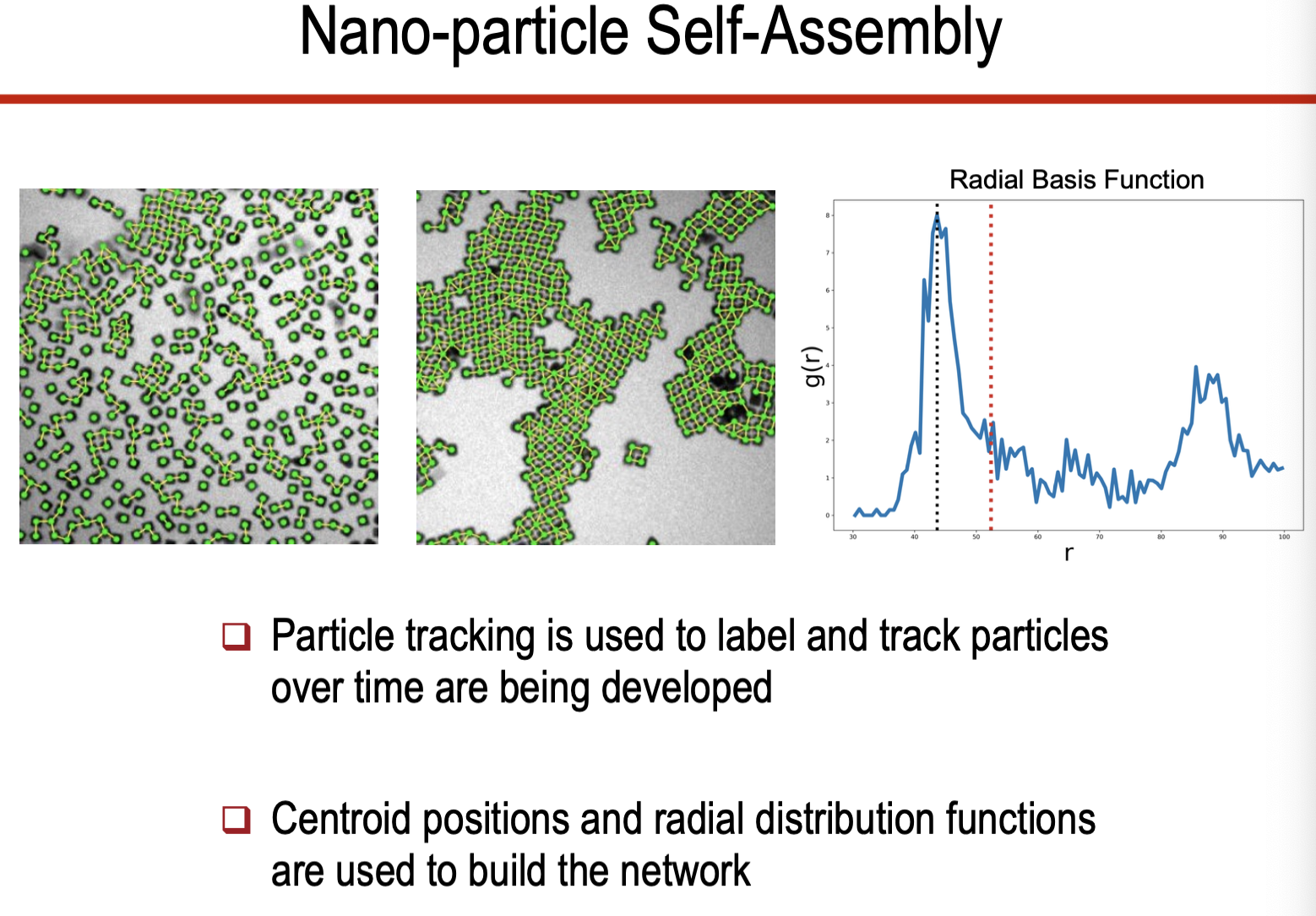
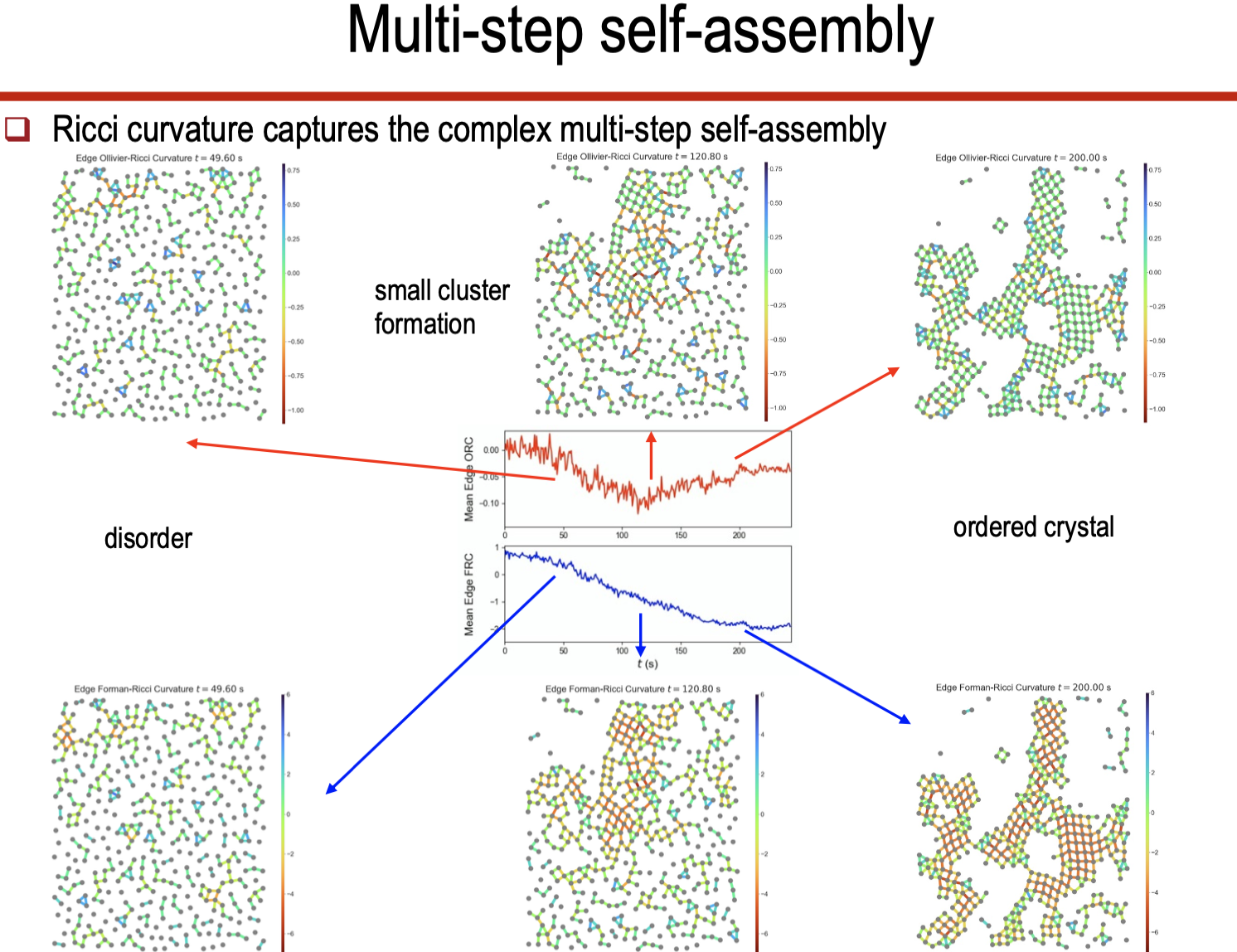
• 나노 물질 자기조립(Self-Assembly)
  • 나노 입자의 다단계 조립 과정에서 FRC를 사용.
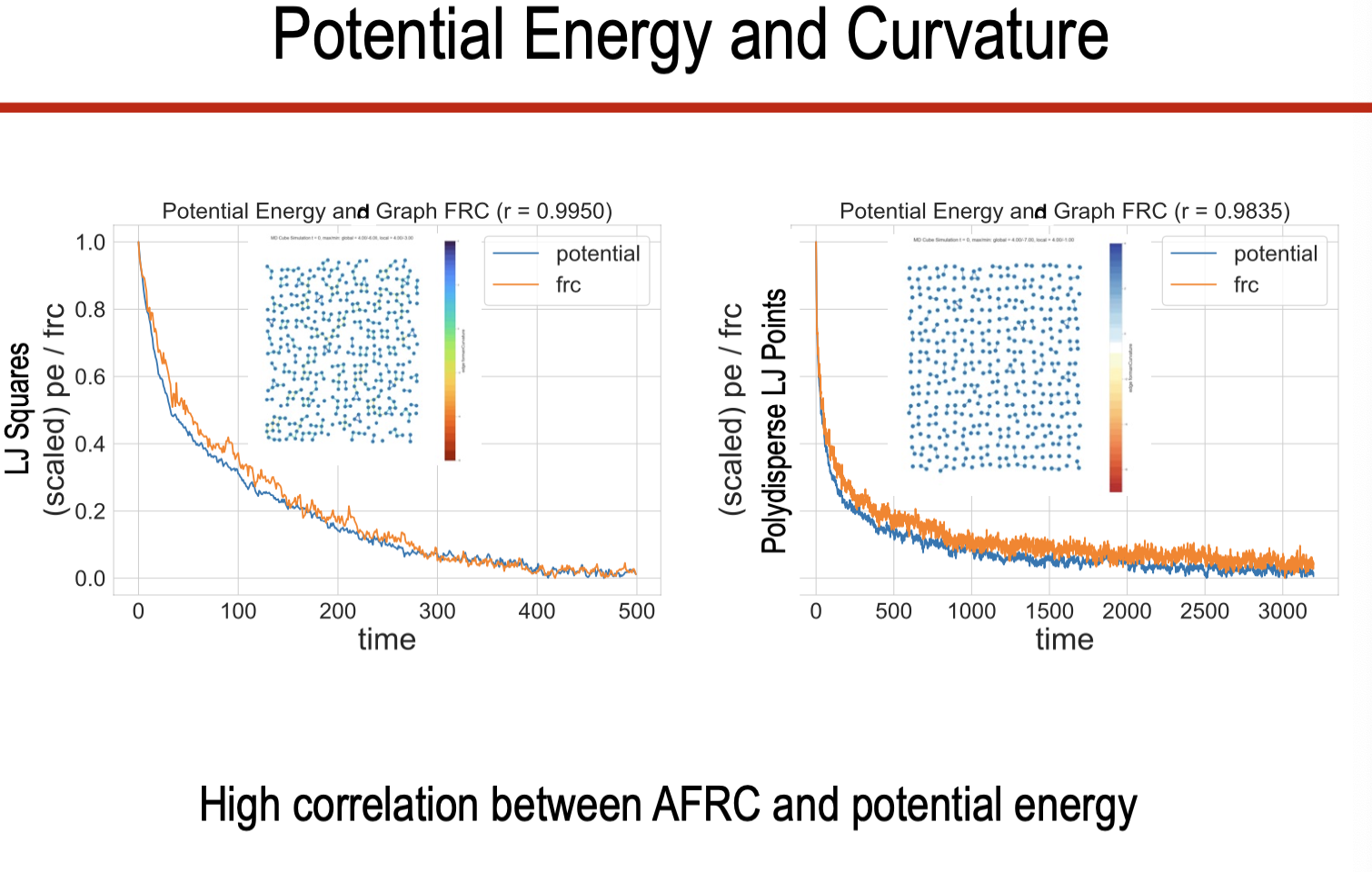
  • 엔트로피 변화는 잠재 에너지와 높은 상관관계를 보인다.

출처: Lecture 6 slides

• 사이버 물리 시스템(Cyber Physical Systems)
  • 하드웨어-소프트웨어 설계 최적화에 활용.
  • 자율 시스템의 경로 계획과 안정성 분석.
• 딥러닝 모델
  • 딥러닝 네트워크의 학습 과정에서 FRC를 사용하여 위상 변화를 감지.
  • 학습 초기 과적합 방지와 최적 학습 단계를 찾는 데 활용.

---

결론

Forman-Ricci Curvature는 네트워크의 구조적 변화를 탐지하고 복잡한 시스템의 동역학적 패턴을 분석하는 데 강력한 도구로 자리잡는다.
다양한 실험과 실제 데이터에서 FRC는 효율적이고 정밀한 결과를 제공하며, 과학, 공학, 데이터 분석 전반에서 유망한 응용 가능성을 보여주고 있다.