(Lecture 3) Multifractals and Graph Higher-Order Statistics

Multifractals와 Multifractal Analysis

 

개요

이 강의에서는 Multifractal 이론과 그래프의 고차 통계 분석을 다룹니다. 주요 내용은 다음과 같습니다:

    1. Multifractal의 정의와 특성

    2. Hierarchical Resistor Network (HRN) 모델

    3. Mass Exponent와 Generalized Fractal Dimension

    4. Lipschitz-Hölder Exponent와 Multifractal Spectrum

    5. Multifractal Detrended Fluctuation Analysis (MFDFA)

    6. 복잡한 네트워크에서의 Multifractal 분석

 

 

1. Multifractal의 개념

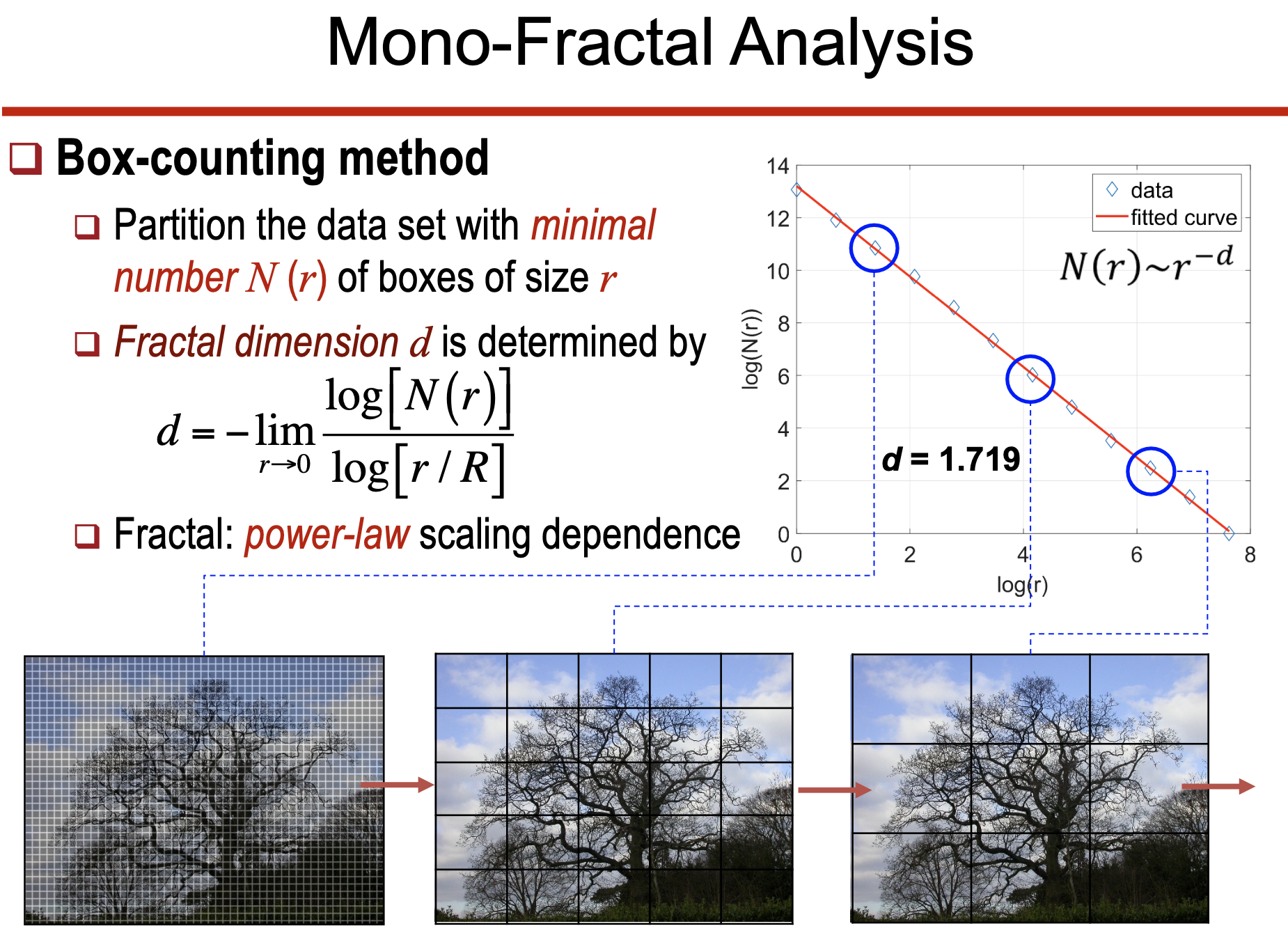
• Mono-fractals vs. Multi-fractals

    • Mono-fractals: 단일 프랙탈 지수로 설명됨.

    • Multi-fractals: 다양한 프랙탈 지수를 가지며, 더 복잡한 구조를 나타냄.

    • 예시: 주식 시장, 난류, 생물학적 시스템, 지질학.

• Multifractal의 정의

    • 공간 상에서, 크기 는 반경 에 따라 다음과 같이 스케일링됨:

    • : 각 위치에서의 지역 스케일링 지수.

• Multifractal Spectrum

    • 의 분포를 로 정의:

여기서 는 Mass Exponent.

 

출처: (좌)https://www.nature.com/articles/s41586-024-07287-2 , (중) https://sohl-dickstein.github.io/2024/02/12/fractal.html, (우) https://antenna-theory.com/antennas/fractal.php

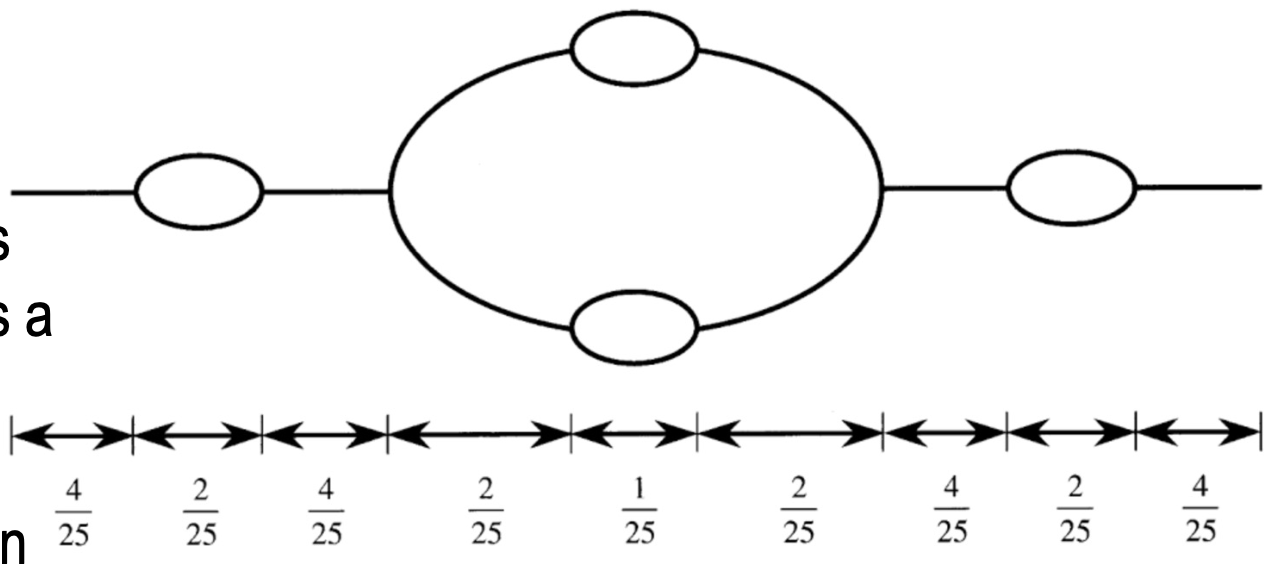
2. Hierarchical Resistor Network (HRN) 모델

• 모델 구성

    • 기본 저항 네트워크를 기반으로 반복적인 self-similar 구조 생성.

    • 특정 세대에서의 전압 강하 분포와 통계적 모멘트 분석.

• 수식

    • 전압 강하 와 결합 수 :

    • 통계적 모멘트는 다음과 같은 스케일링 법칙을 따름:

 

3. Mass Exponent와 Generalized Fractal Dimension

• Mass Exponent

여기서 은 Box Counting Measure.

 

 

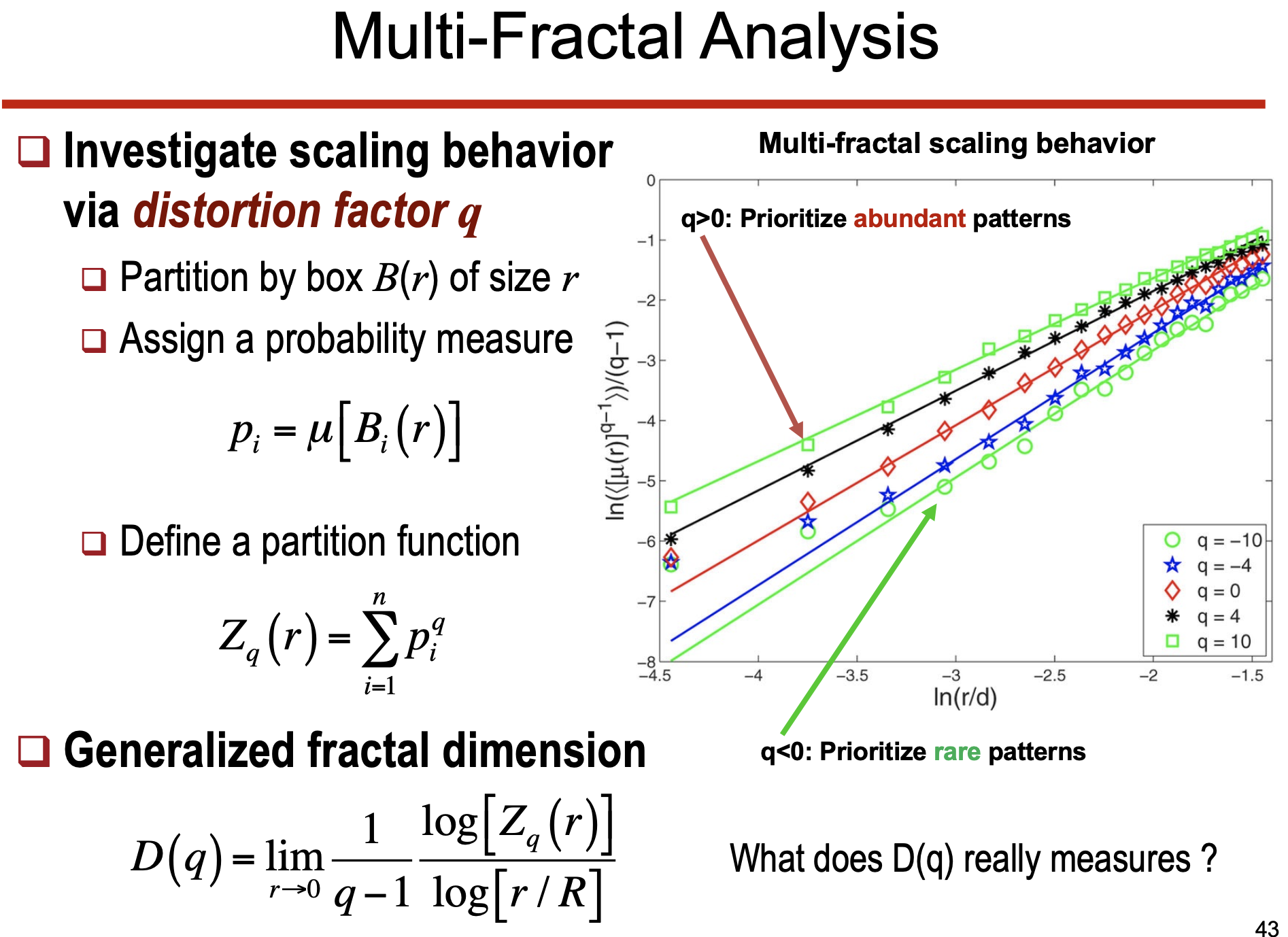
• Generalized Fractal Dimension

    • 와의 관계로 정의됨:

 

4. Lipschitz-Hölder Exponent와 Multifractal Spectrum

• Lipschitz-Hölder Exponent

$\alpha(q) = \frac{d \tau(q)}{dq}$

• Multifractal Spectrum

    • 와 는 Multifractal의 구조적 다양성을 나타냄.

 

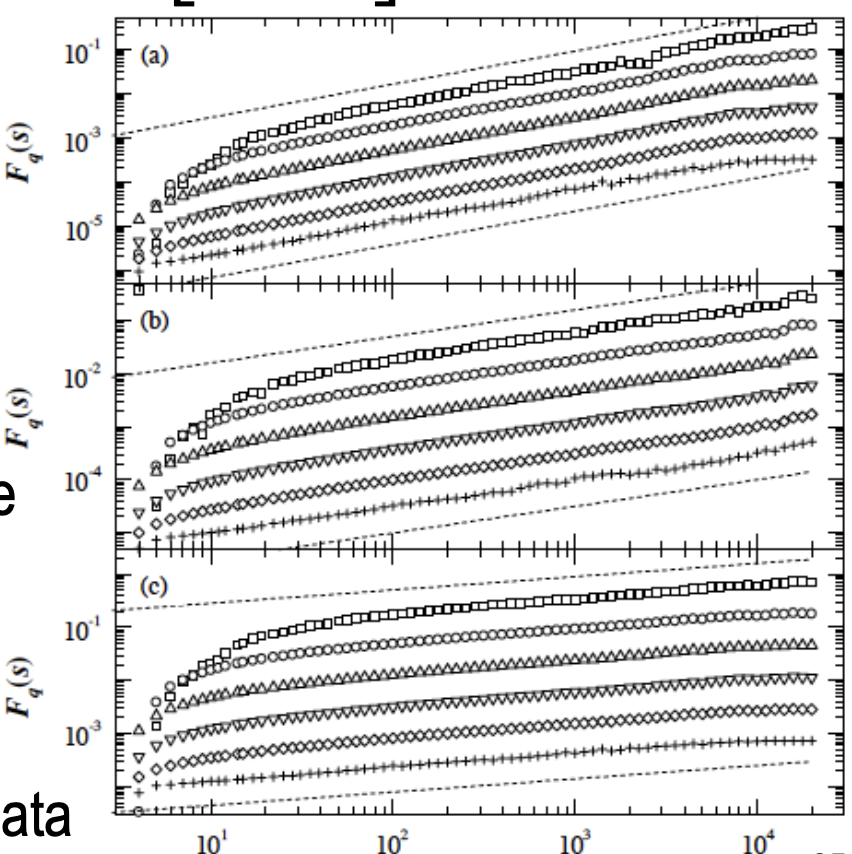
5. Multifractal Detrended Fluctuation Analysis (MFDFA)

    1. 시간 시퀀스를 박스 크기 로 나누고 로컬 트렌드 제거.

    2. 차 플럭추에이션 함수 계산:

    3. 과 의 기울기를 통해 도출:

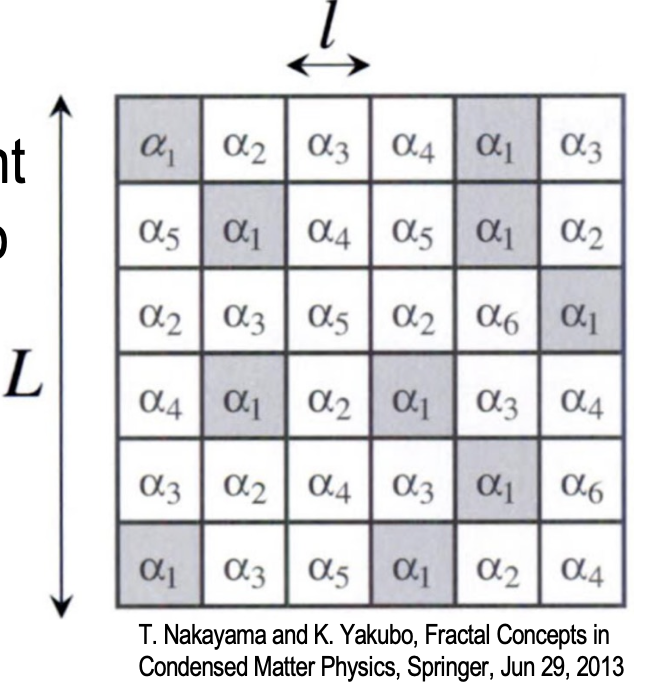
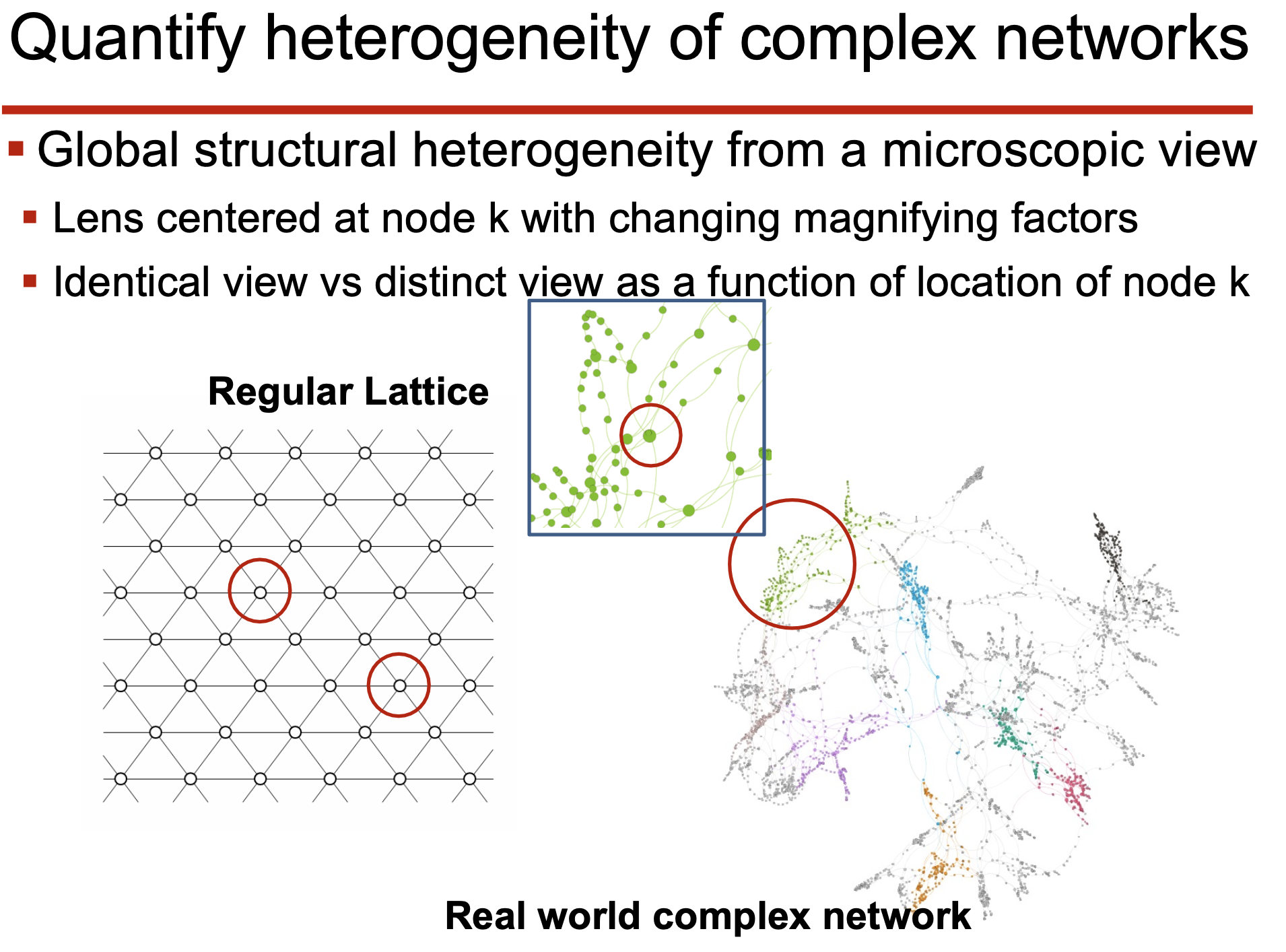
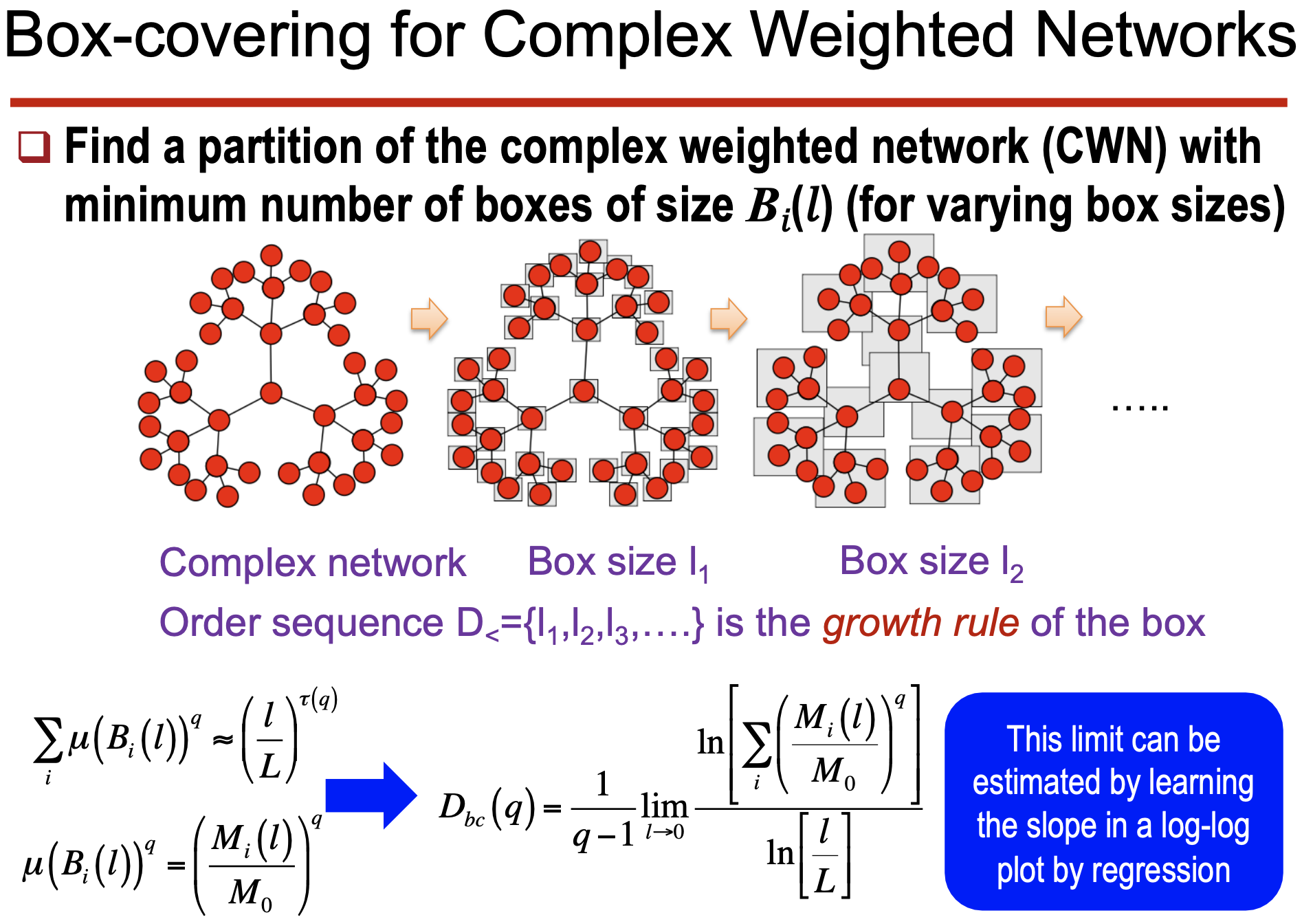
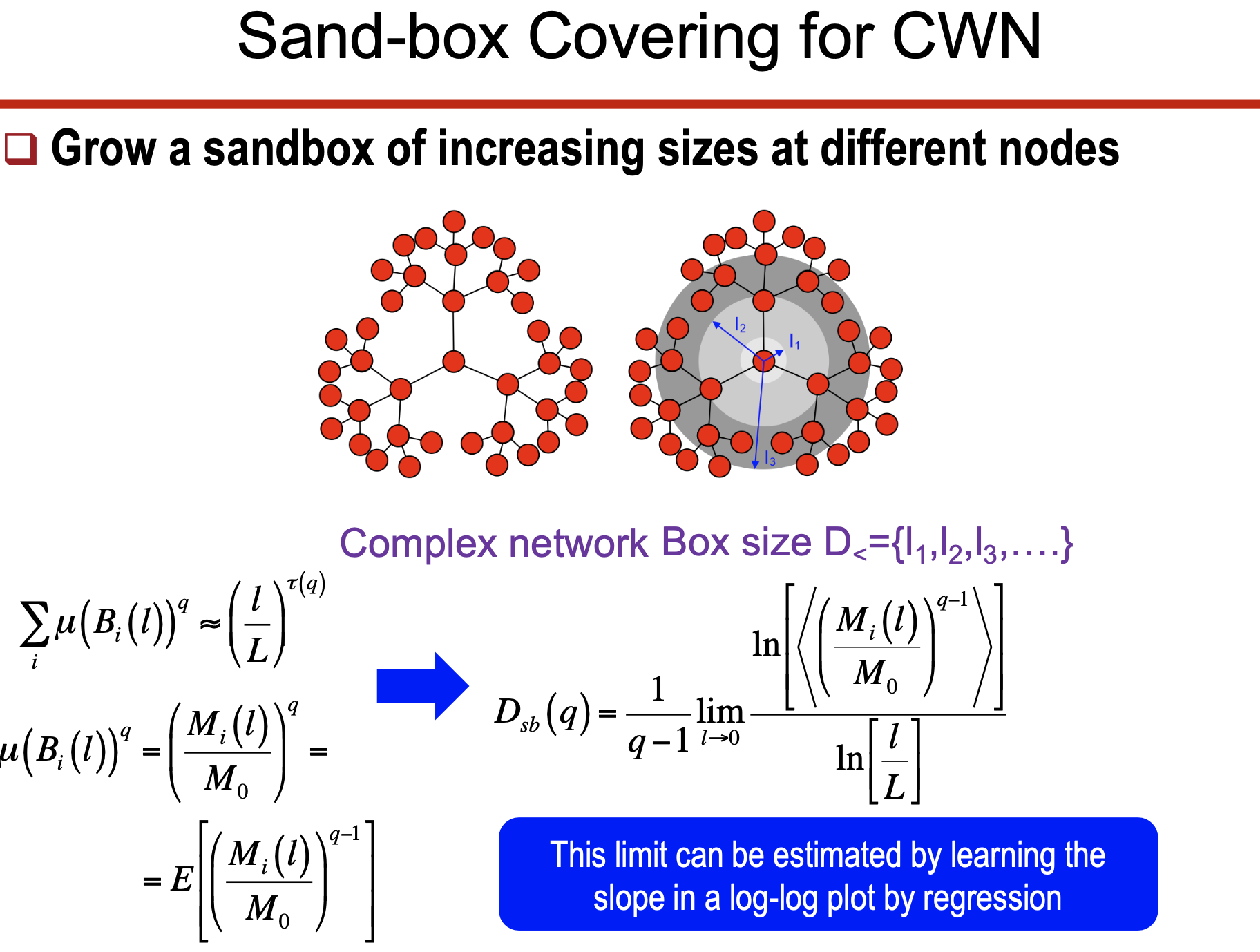
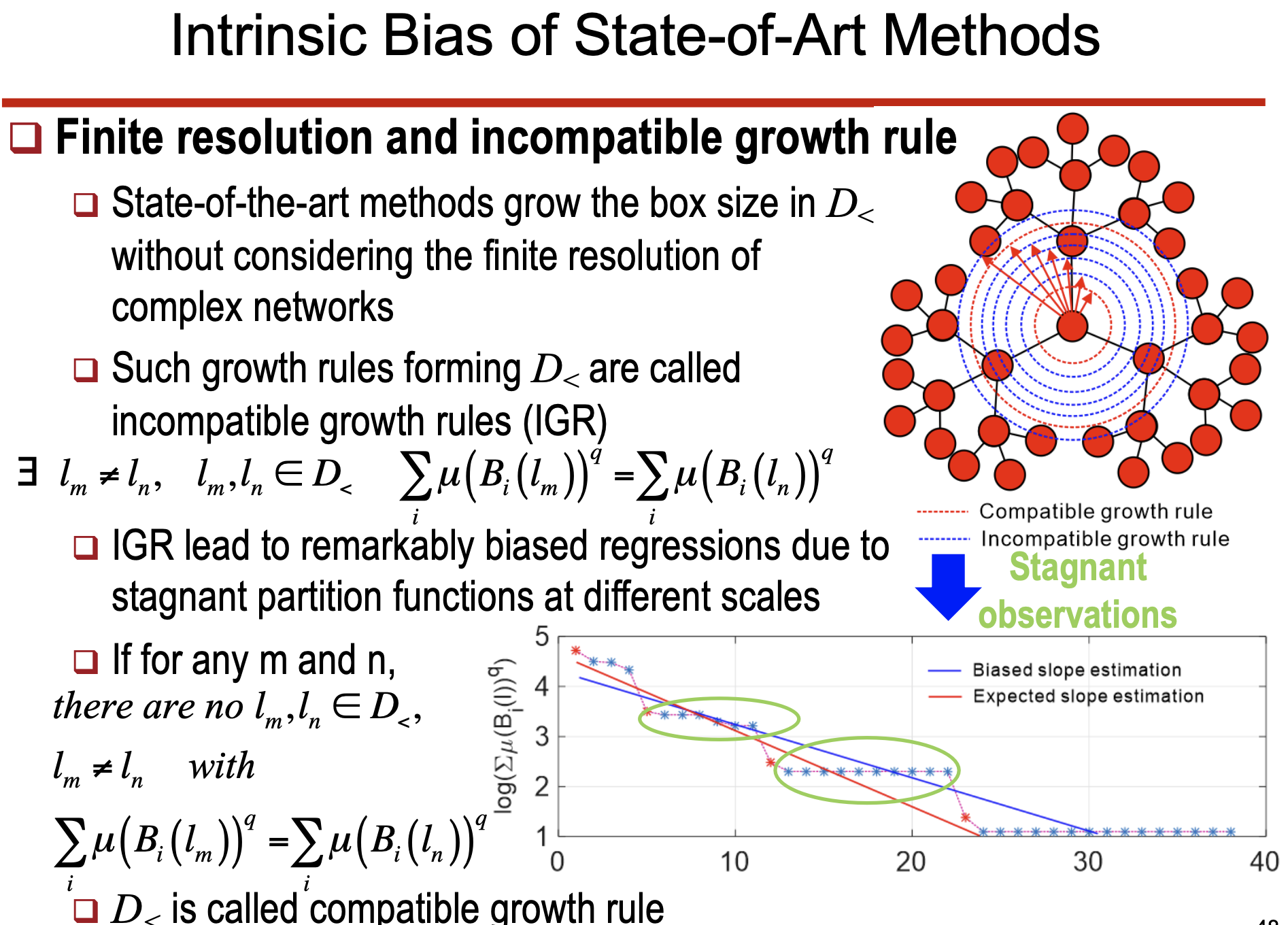
6. 복잡 네트워크에서의 Multifractal 분석

• 네트워크 상자 분할

    • 박스 크기 로 네트워크를 분할하고, 각 박스의 확률 측정 를 정의.

    • Mass Exponent와 Generalized Fractal Dimension 추정:

• Legendre 변환

,

 

주요 특징

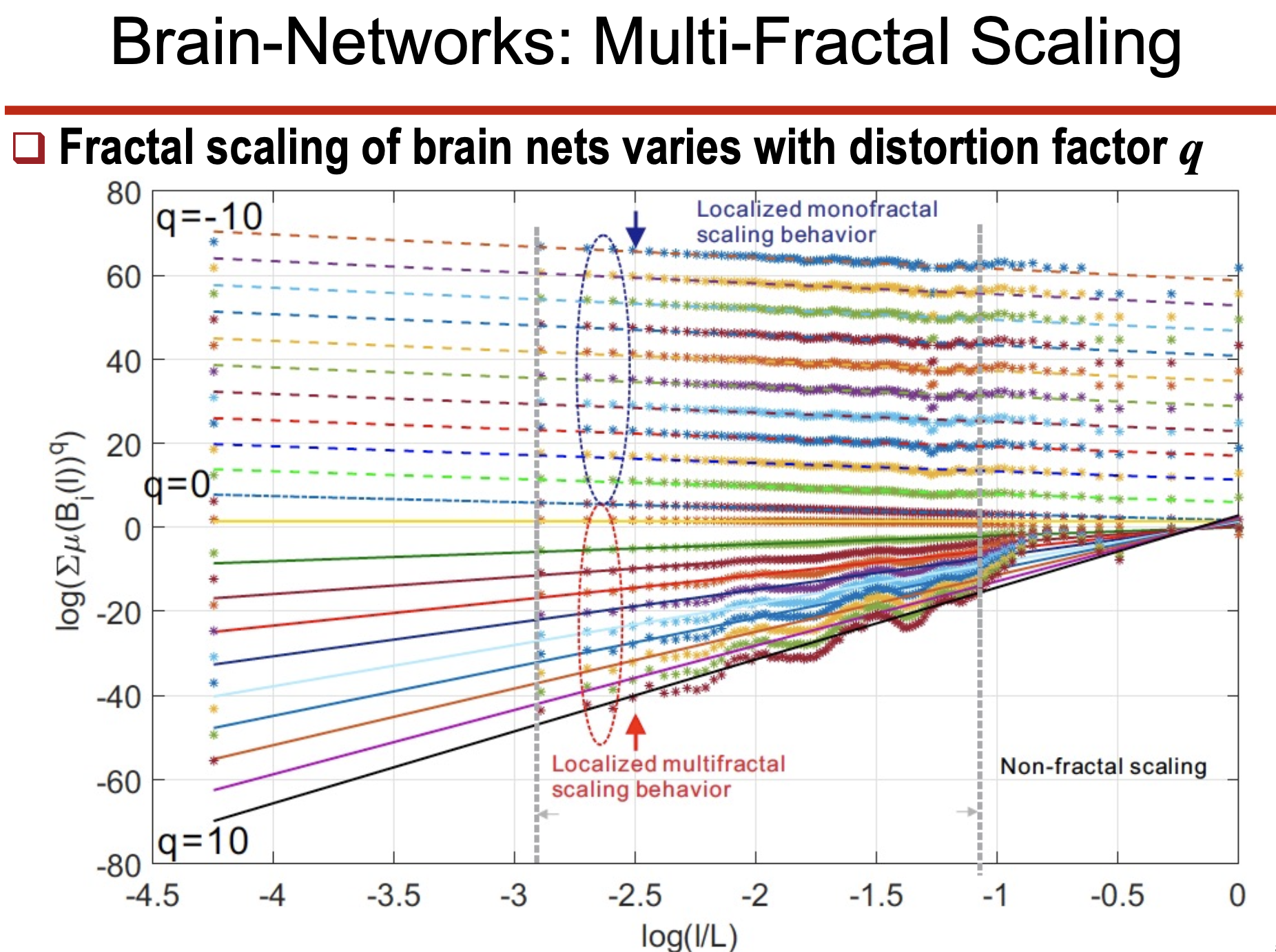
• Multifractal은 단순한 Mono-fractal 모델보다 복잡한 데이터의 스케일링 특성을 잘 설명.

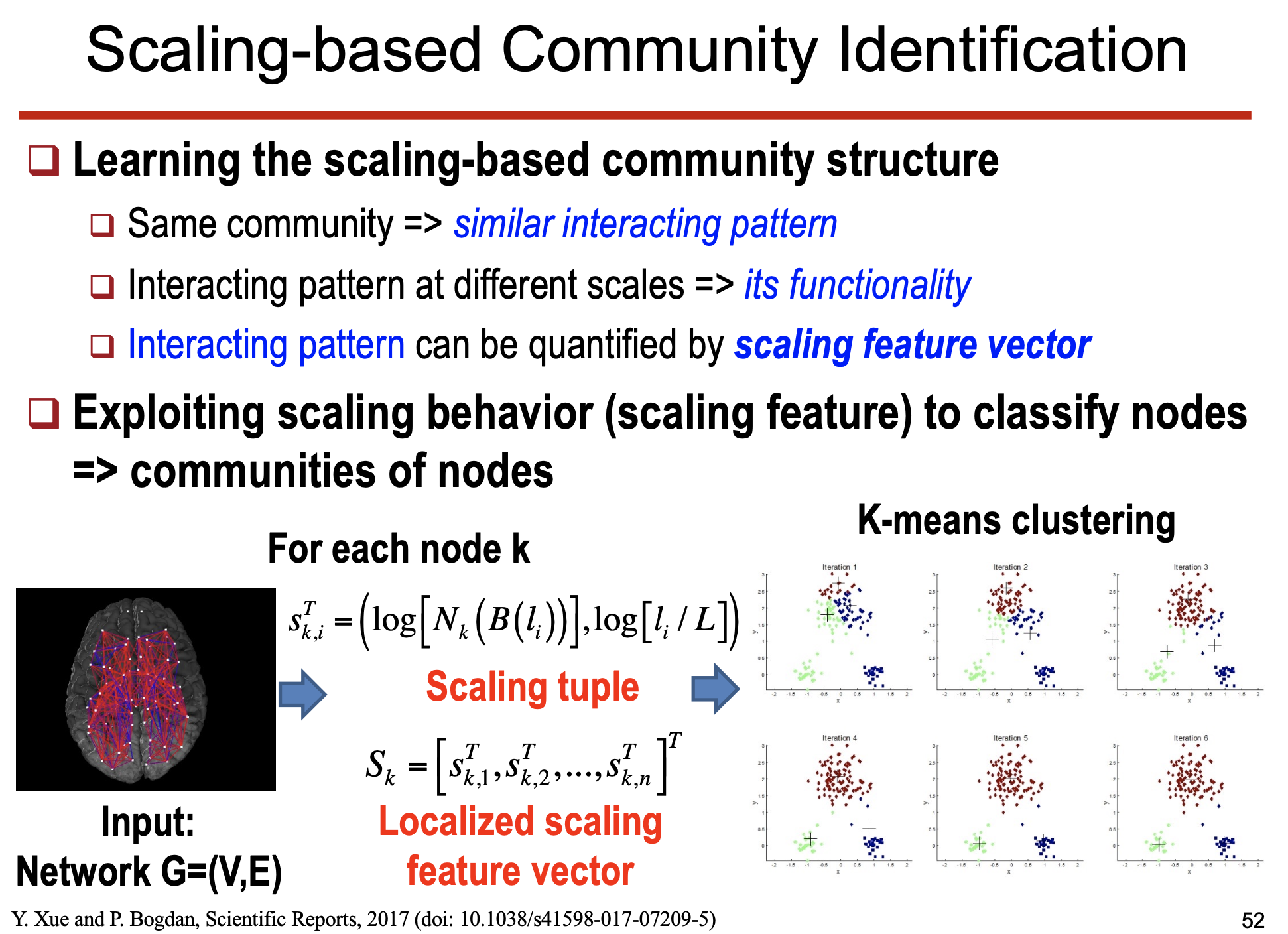
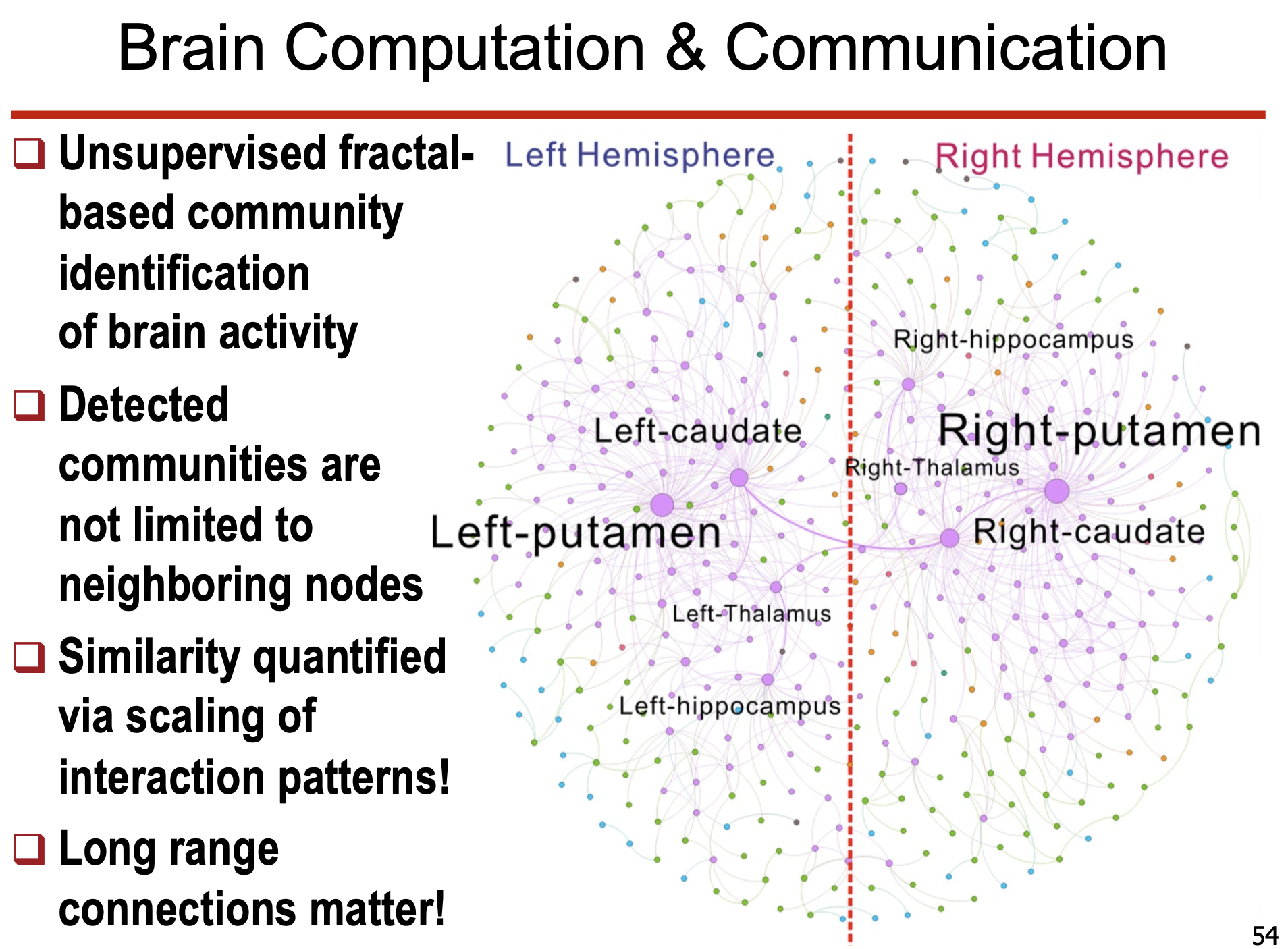
• 다양한 실험적 데이터 (뇌 네트워크, 금융 데이터 등)에서 Multi-fractal 특성을 확인.

• MFDFA는 Multifractal 특성을 정량화하는 강력한 도구로 활용 가능.

 

강의에서 소개된 이론과 모델은 복잡한 시스템에서의 패턴 분석 및 데이터 모델링에 중요한 기반을 제공.

 

출처: Lecture 3 Slide