728x90
강의 개요
이번 강의에서는 Node-based Multifractal Analysis (NMFA)의 개념과 방법론을 다룬다.
NMFA는 네트워크의 복잡성과 다중 스케일 특성을 분석하며, Watts-Strogatz 네트워크의 위상 전이와 다양한 응용 가능성을 탐구한다.

1. Fractal Analysis
- 프랙탈 정의
프랙탈은 자기유사성을 가지며, 각 부분이 전체의 축소된 버전으로 간주된다. - 프랙탈 차원 계산
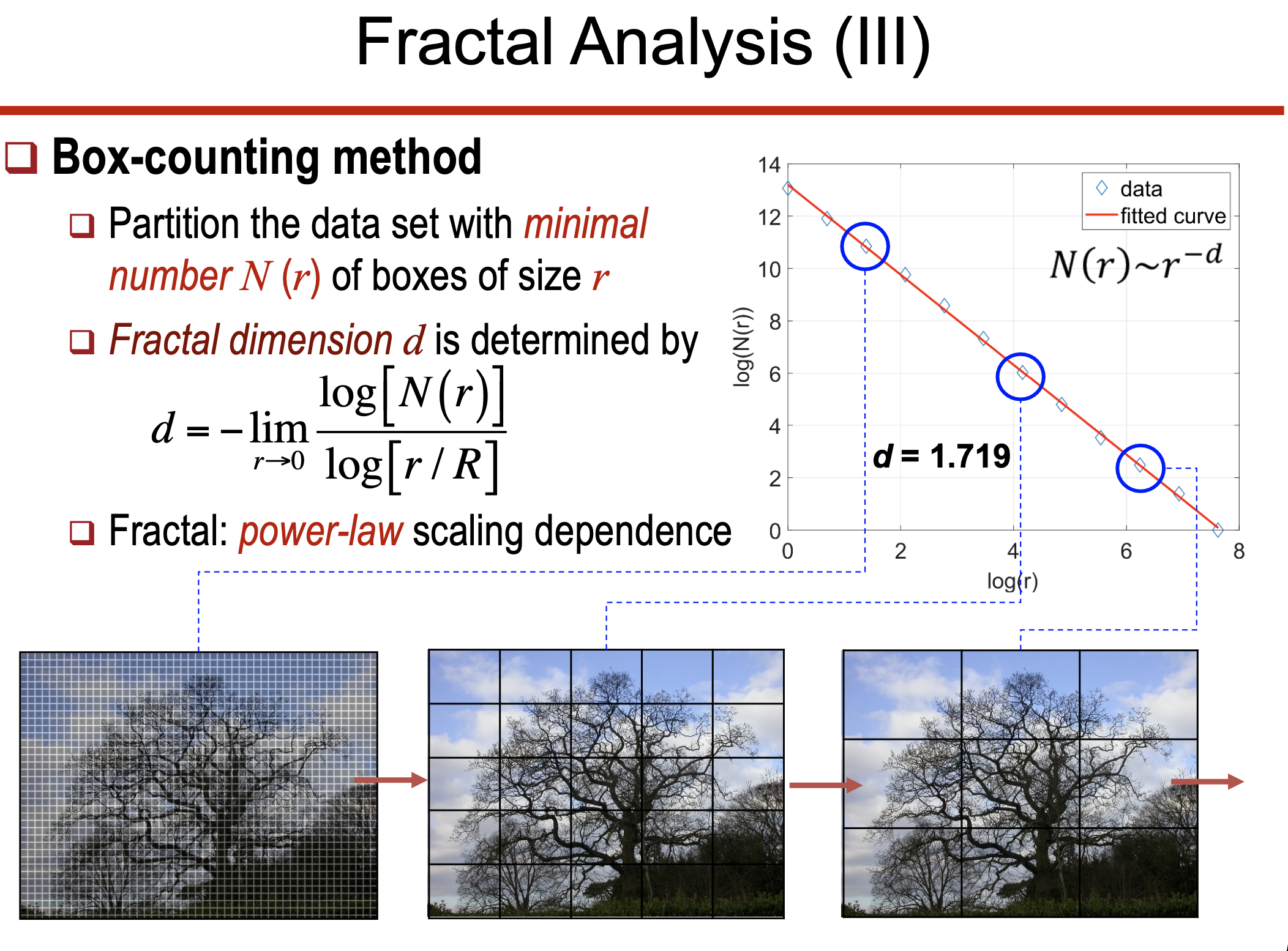
Box-counting 방법을 통해 프랙탈 차원을 계산하며 다음 관계를 따른다:
$ D = \lim_{r \to 0} \frac{\log N(r)}{\log(1/r)} $
여기서 $ N(r) $은 크기 $ r $의 박스 수를 의미한다.


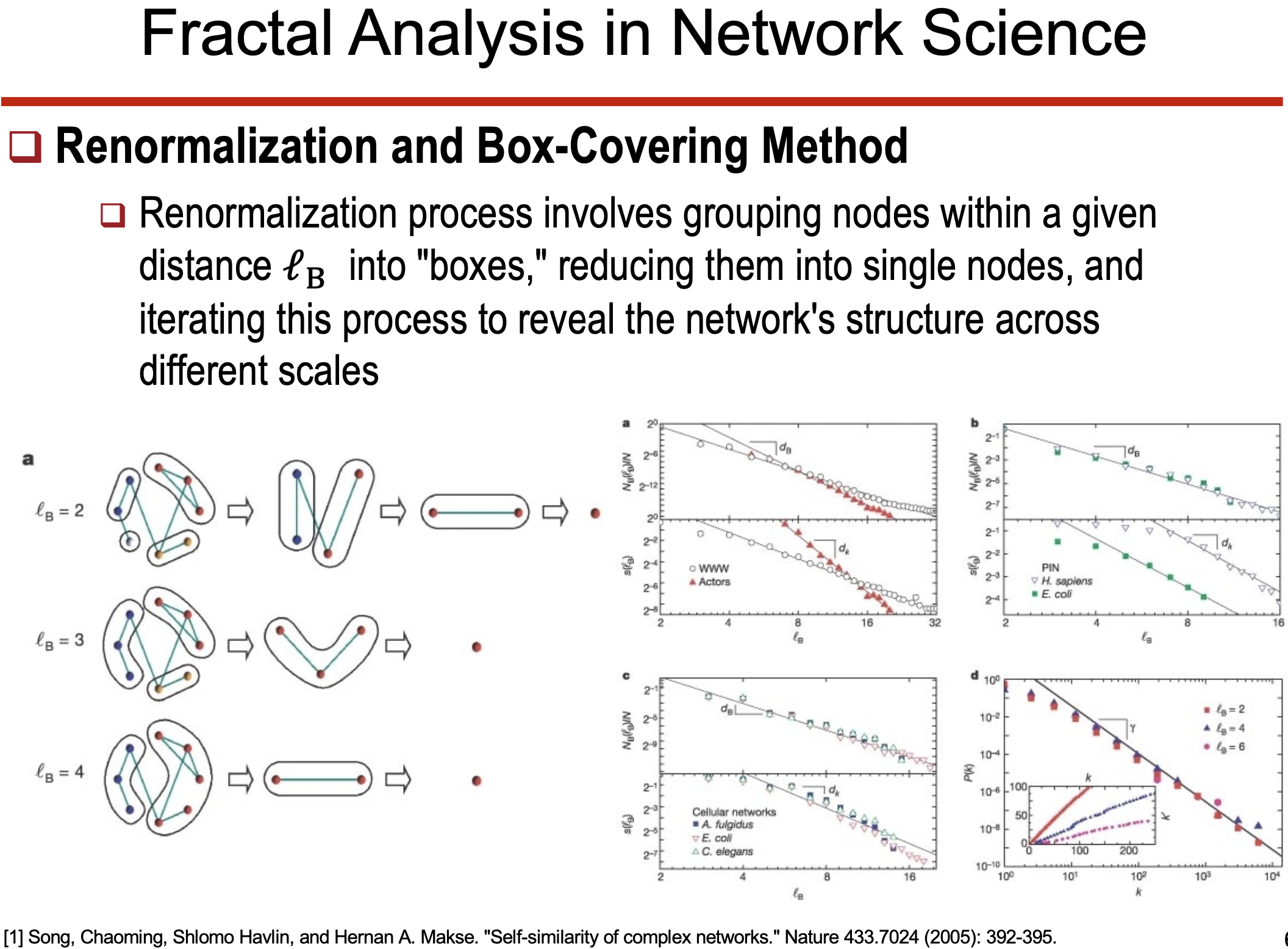
- 네트워크에서의 프랙탈 분석
Renormalization과 Box-covering 방법을 사용하여 네트워크의 스케일별 구조를 분석한다.
2. Multifractal Analysis
- Mass Exponent ($\tau(q)$)
$ \tau(q) = \lim_{l \to 0} \frac{\log \sum_i \mu_i^q}{\log l} $
여기서 $\mu_i$는 각 박스의 확률 측정값이며, $l$은 박스 크기다. - Generalized Fractal Dimension ($D_q$)
$ D_q = \frac{\tau(q)}{q-1} $
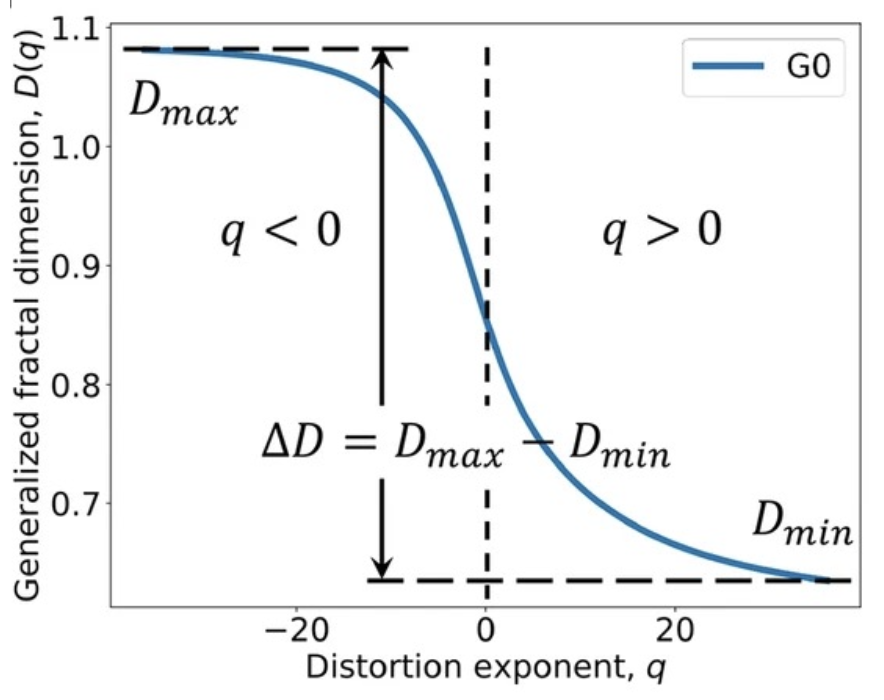
- Lipschitz-Hölder Exponent ($\alpha(q)$)
$ \alpha(q) = \frac{d \tau(q)}{dq} $
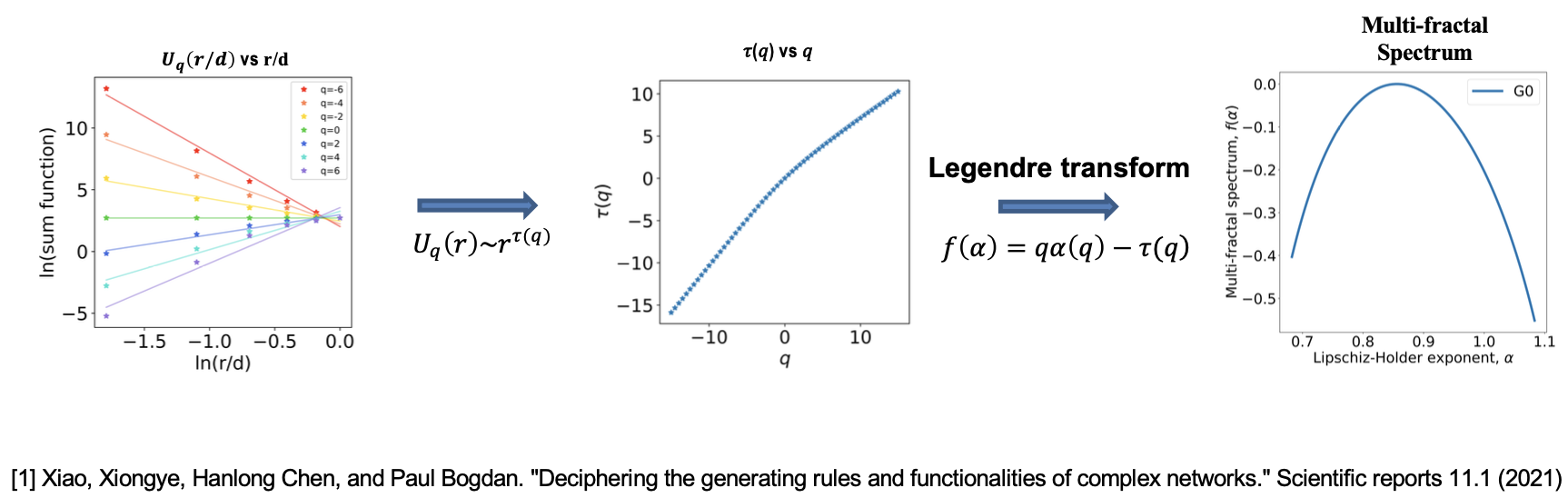
- Multifractal Spectrum ($f(\alpha)$)
$ f(\alpha) = q \alpha - \tau(q) $
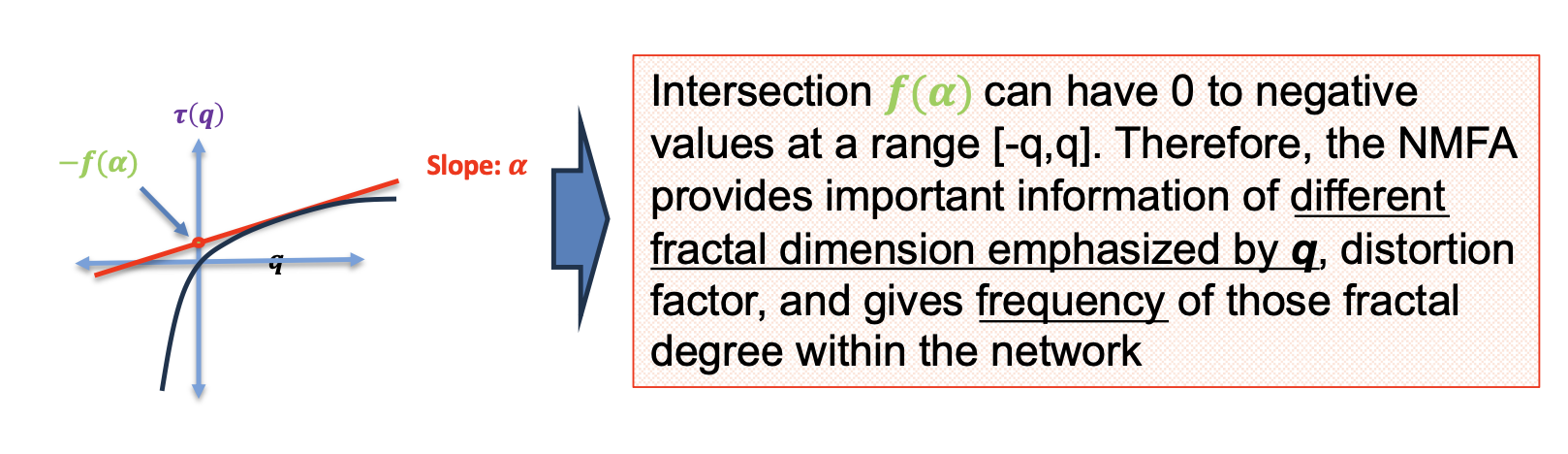

3. Node-based Multifractal Analysis (NMFA)
- 방법론
- 노드 기반의 프랙탈 차원 계산: 특정 노드를 중심으로 Box-growing 방법을 사용.
- Topological Partition Function 도입:
$ U_q(r) = \sum_i \mu_i^q $
왜곡 계수 $q$를 사용해 패턴의 희소성과 빈도를 강조. - Multifractal Scaling Behavior 분석:
$ U_q(r) \sim r^{\tau(q)} $
- NMFA의 장점
- 기존 Box-covering 방법보다 강건한 결과 제공.
- 다양한 $q$ 값에 따른 패턴 강조로 네트워크 복잡성의 상세 분석 가능.
4. Watts-Strogatz 네트워크에서의 분석
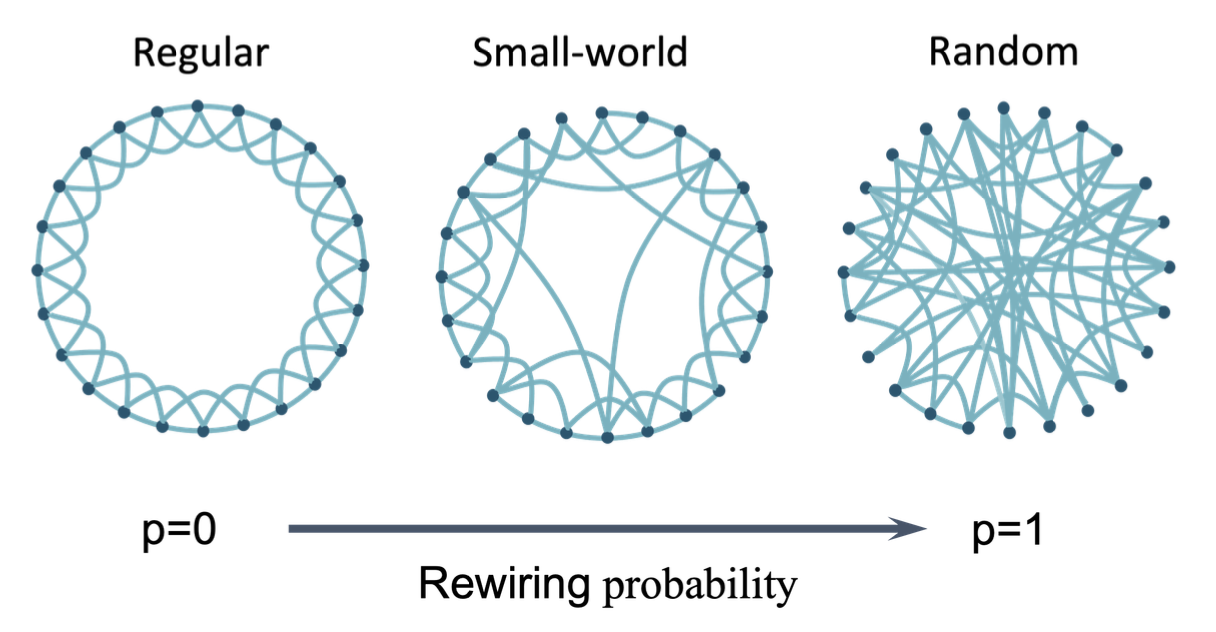
- 특징
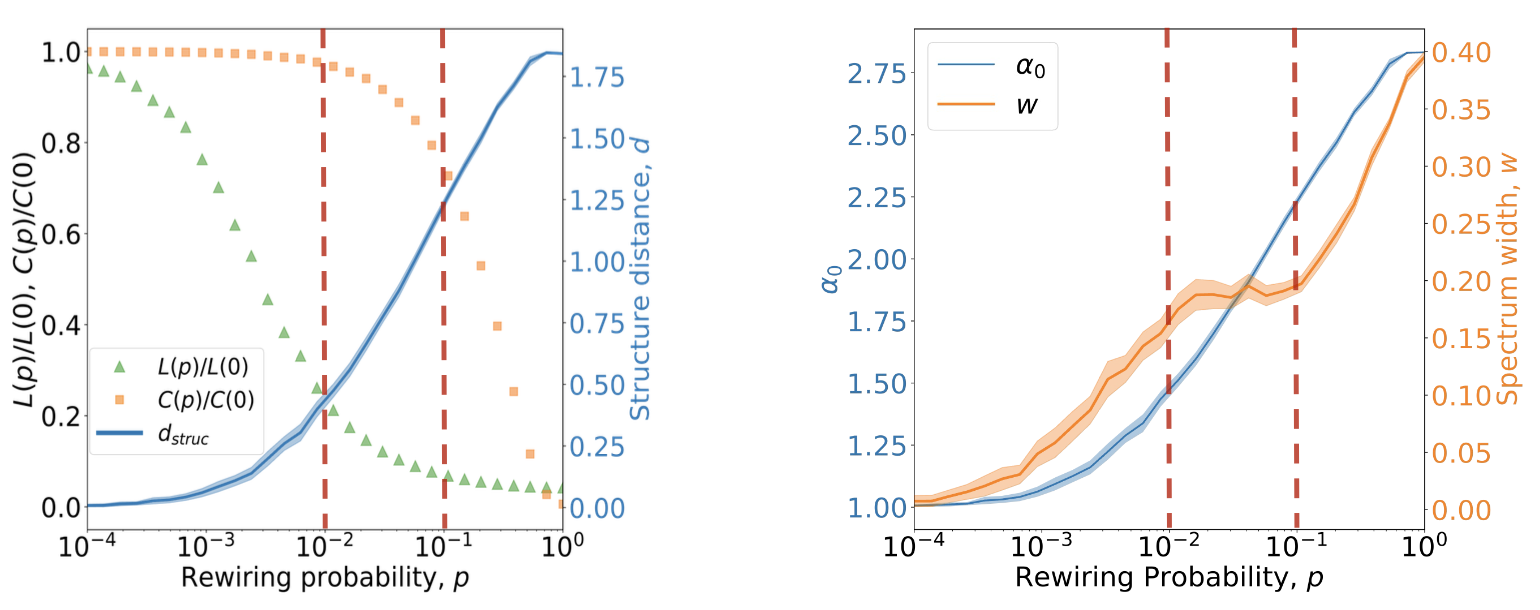
Watts-Strogatz 모델은 높은 클러스터링과 짧은 평균 경로 길이를 특징으로 한다. - NMFA로 분석
네트워크의 위상 전이와 동역학적 변화를 파악한다.- 단일 프랙탈에서 다중 프랙탈 구조로의 전환을 확인.
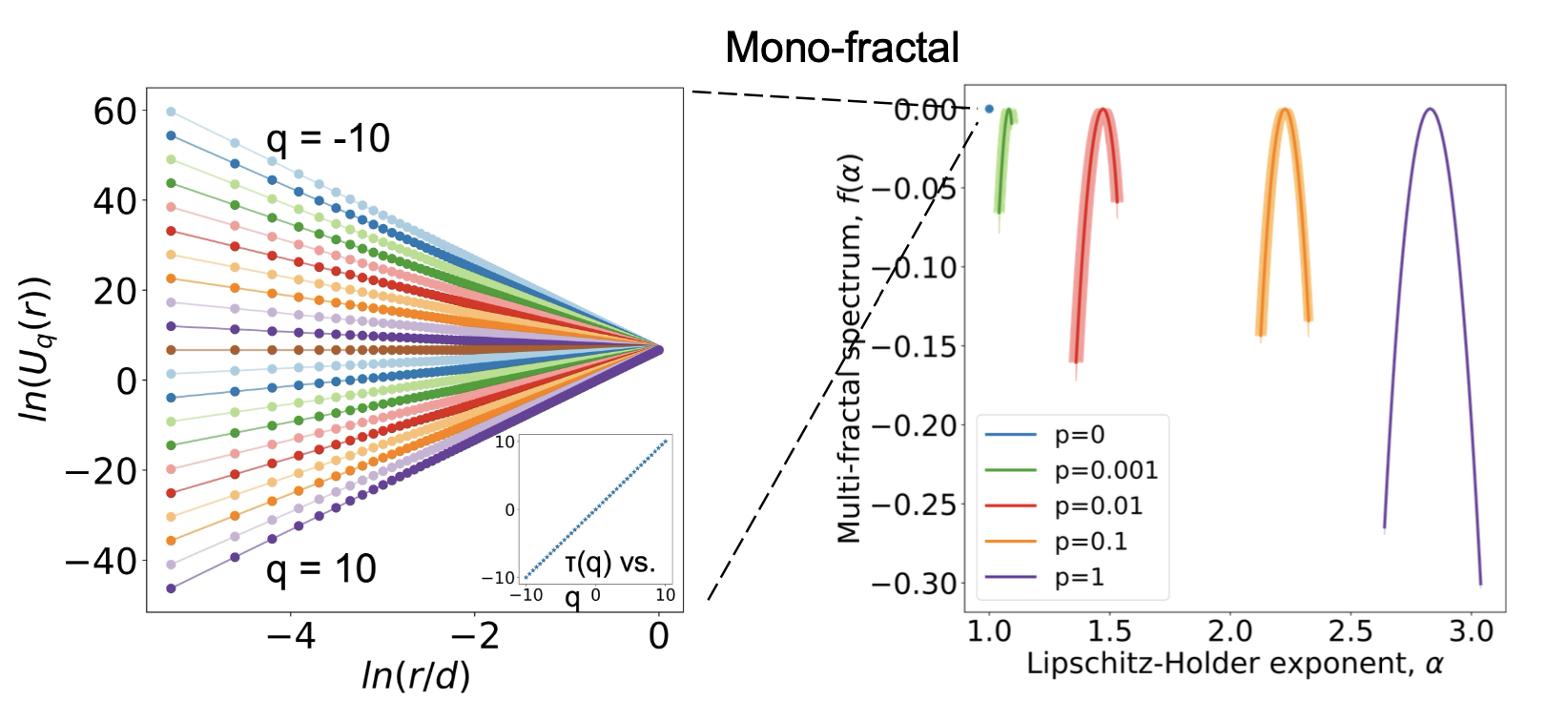
5. 응용 분야
- 신경 과학
NMFA를 사용하여 뇌 네트워크의 복잡성과 기능적 연결성을 분석한다.- 예: 초파리(Drosophila) 시각 센터 분석.
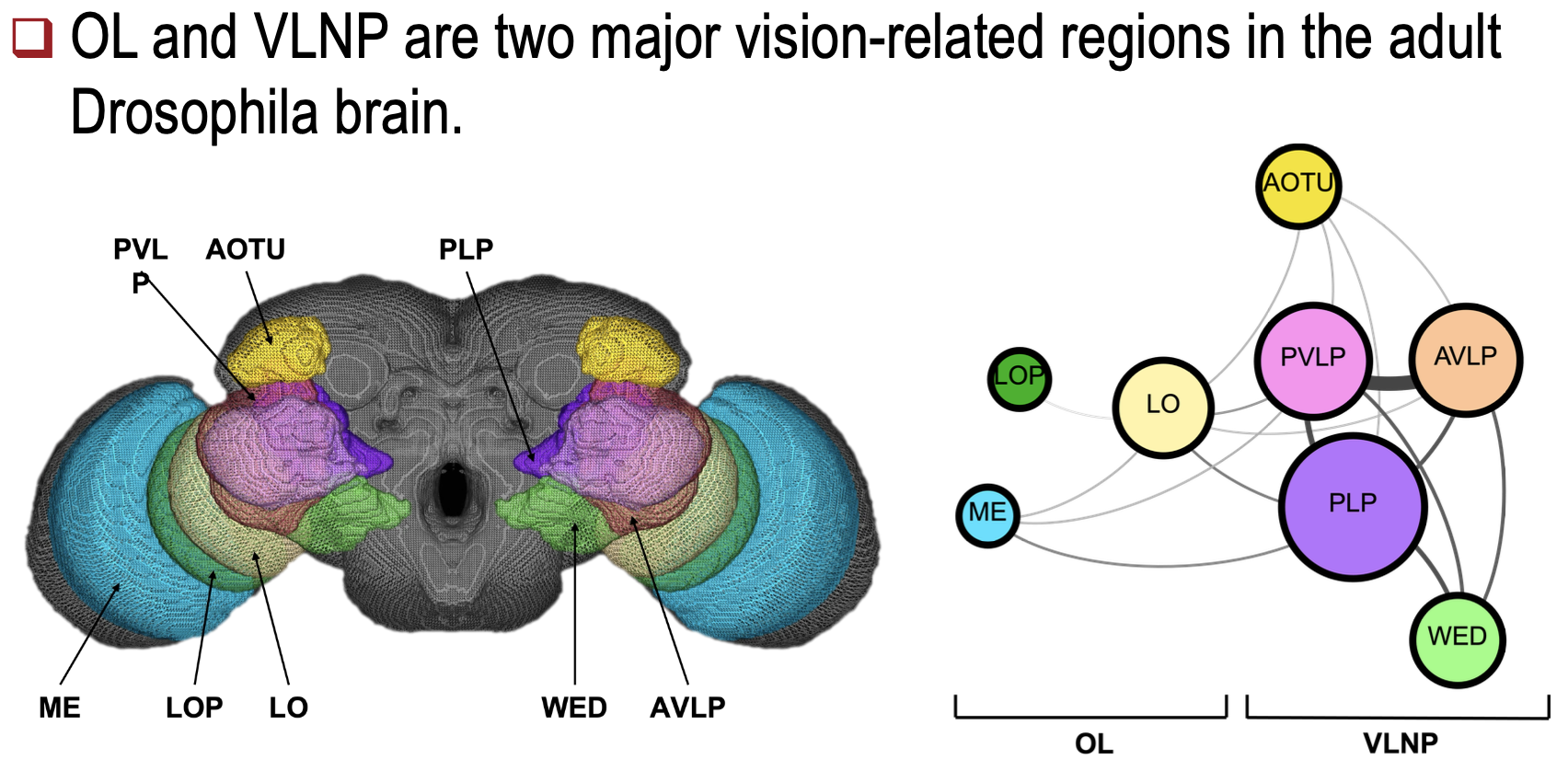
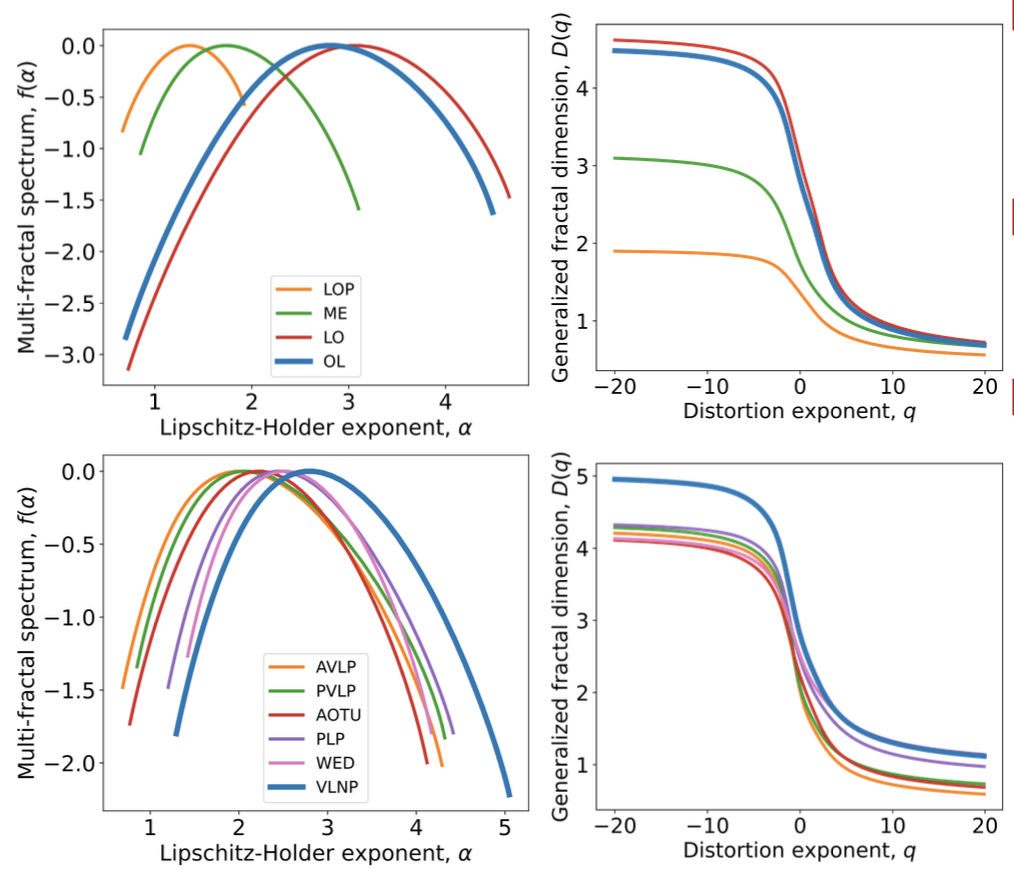
- 물질 과학
NMFA를 통해 나노입자 젤과 비결정 구조의 복잡성을 정량화한다.- 기계적 특성 및 전하 전달 속성과의 상관관계를 연구한다.
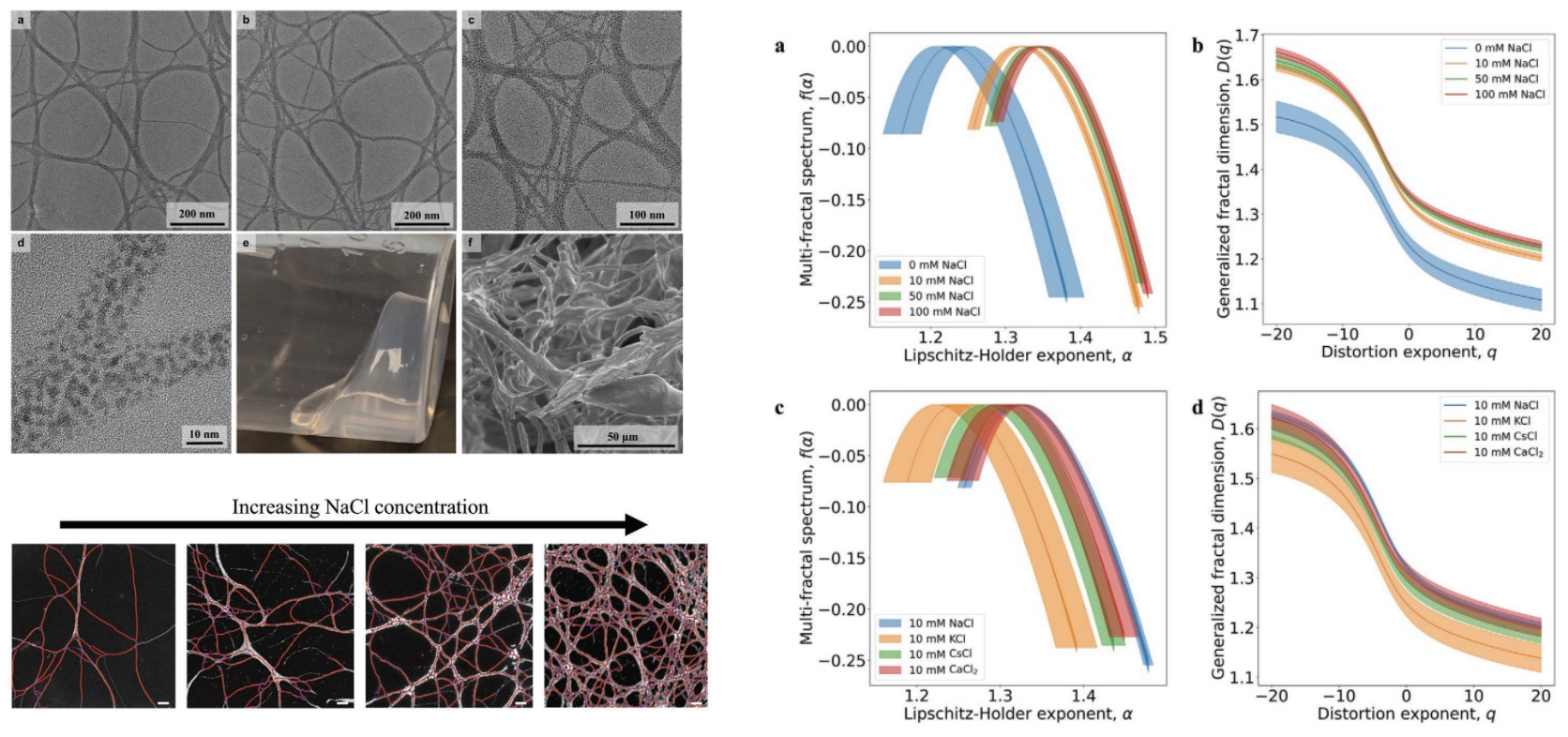
- 생물학적 시스템
단백질-단백질 상호작용 및 약물 설계에 적용된다.
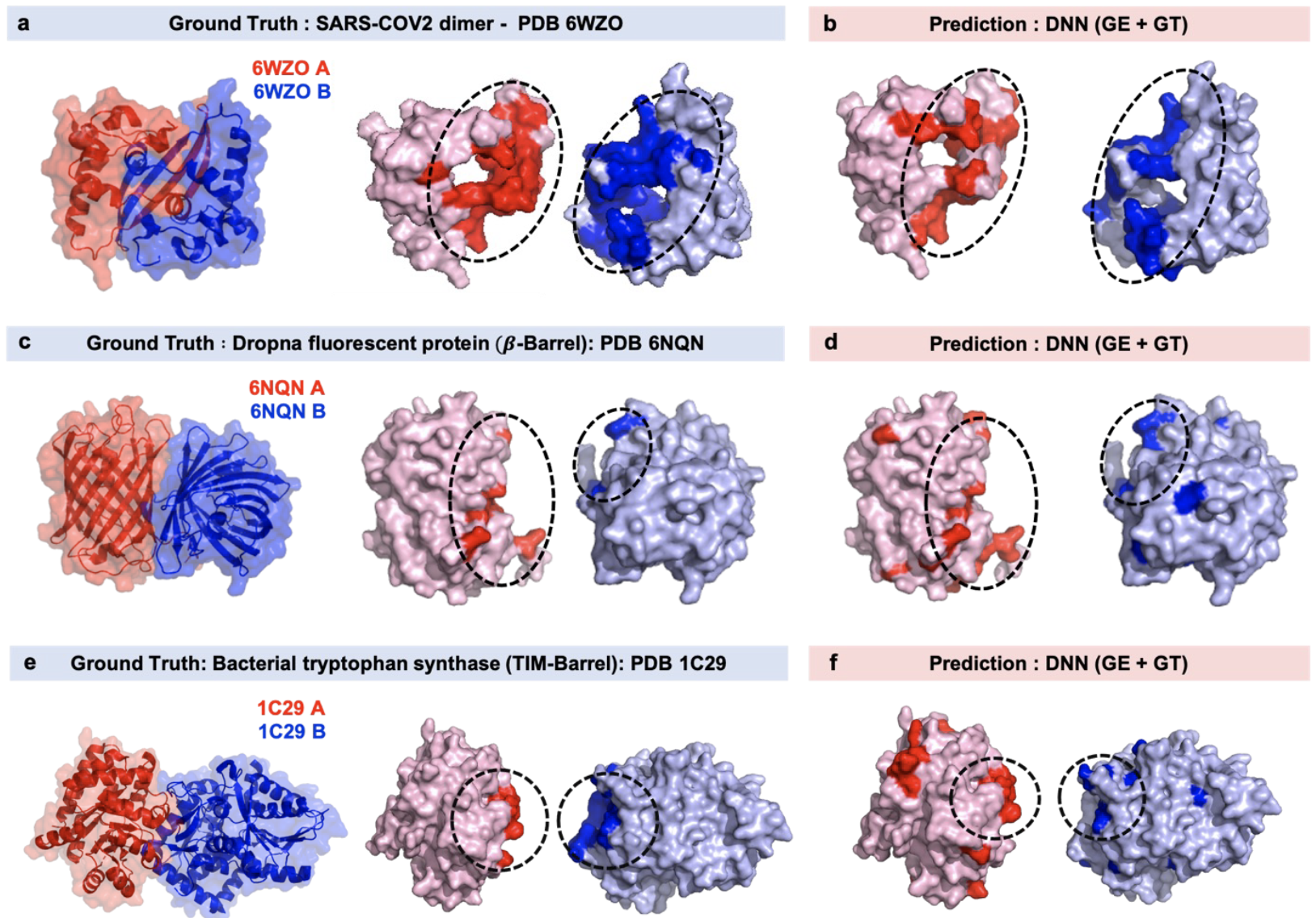
- AI
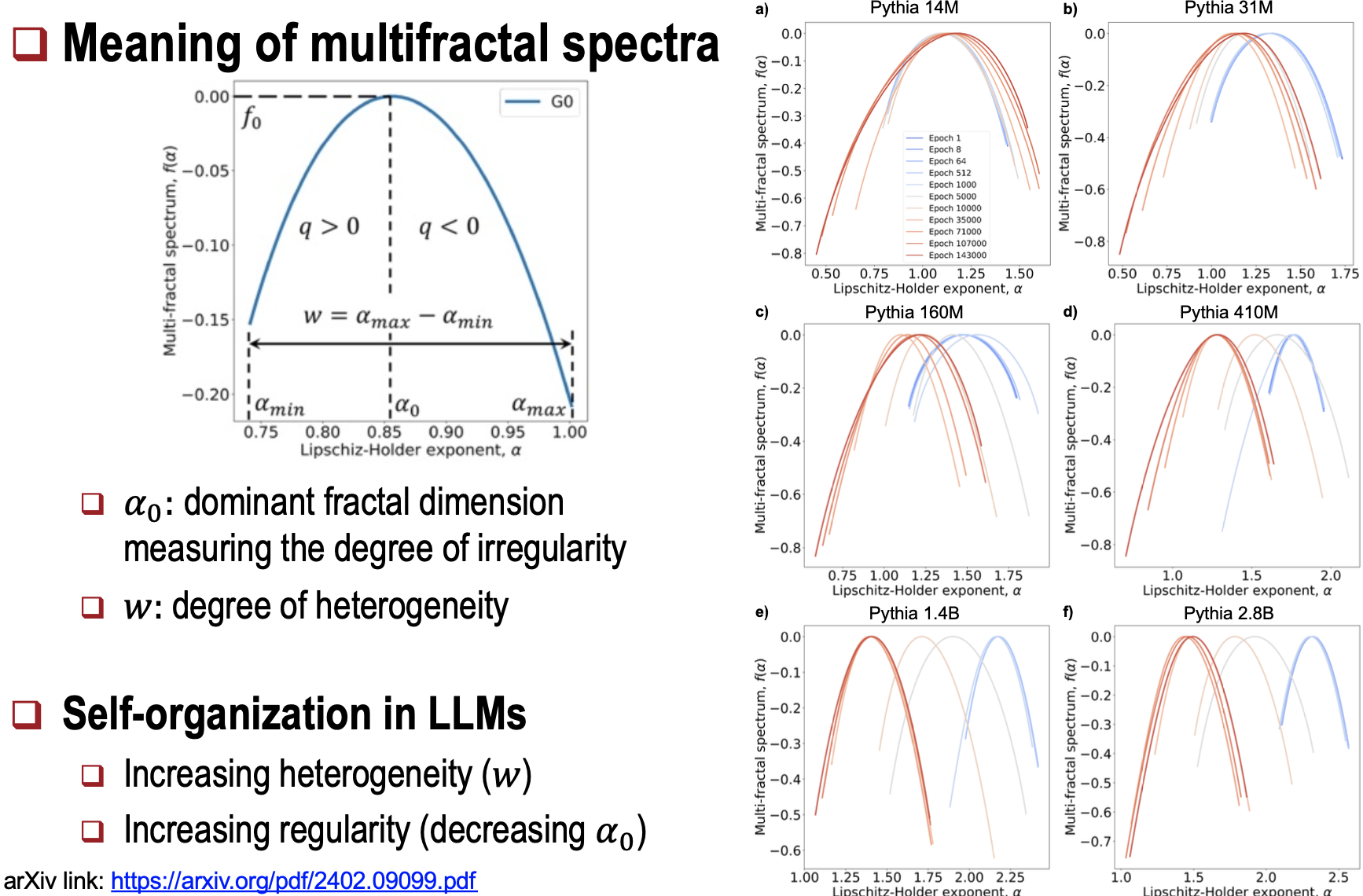
대규모 언어 모델(LLM) 훈련 중 구조적 자기 조직화 및 스펙트럼 분석에 사용된다.
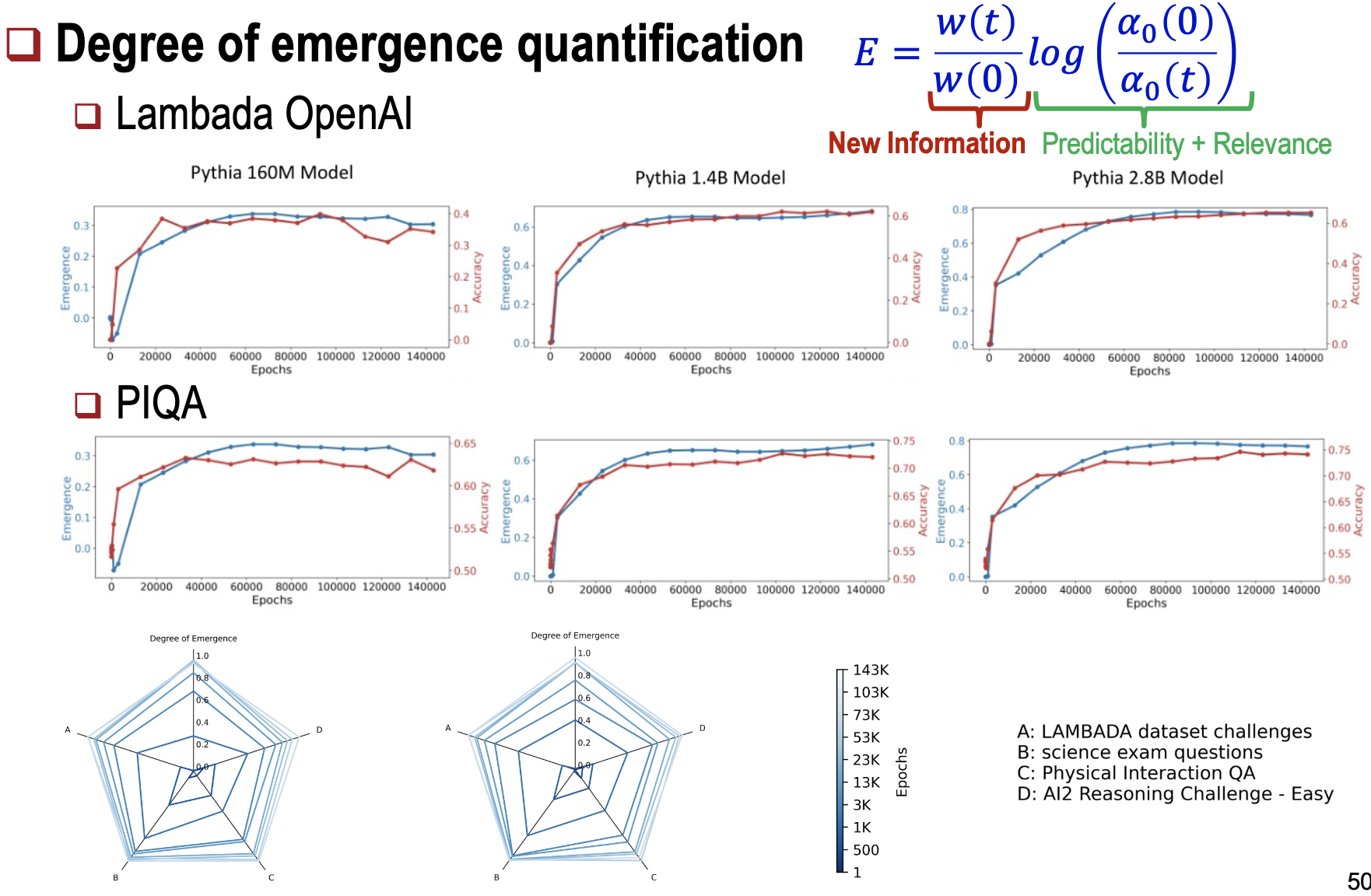
6. 비교 및 결과
- NMFA vs. 기존 방법
- NMFA는 Box-covering 방법보다 희귀 패턴을 더 잘 포착한다.
- Watts-Strogatz 네트워크에서 높은 클러스터링과 경로 길이 분포를 더 정확히 분석한다.
- Multifractal Spectrum 해석
- 스펙트럼의 폭은 네트워크의 이질성을 나타낸다.
- Lipschitz-Hölder 지수 ($\alpha$)는 네트워크 밀도와 복잡성을 특성화한다.
결론
Node-based Multifractal Analysis는 복잡한 네트워크를 분석하는 강력한 도구다. 다양한 응용 분야에서 네트워크 구조와 다중 스케일 동역학을 탐구하며, 강의에서는 이론과 실험적 결과를 통해 NMFA의 효용성을 명확히 제시한다.
728x90
반응형
'Learn > '24_Fall_(EE599) DataScience' 카테고리의 다른 글
| (Lecture 6) Detecting phase transition in time-varying weighted graphs from partial information (0) | 2024.12.22 |
|---|---|
| (Lecture 5) Differential geometry of networks (1) | 2024.12.21 |
| (Lecture 3) Multifractals and Graph Higher-Order Statistics (0) | 2024.12.20 |
| (Lecture 2) Introduction to Graph Theory and Network Science (0) | 2024.12.20 |
| (Lecture 1) Introduction and discussion of project topics (1) | 2024.12.18 |