(Lecture 2) Introduction to Graph Theory and Network Science

1. 그래프 정의와 유형

• 그래프 (Graph)
  그래프 $G = (V, E)$는 다음으로 구성:
  • $V$: 노드(정점) 집합
  • $E$: 엣지(간선) 집합 ($E \subseteq V \times V$)
• 그래프 유형
  • Undirected / Directed: 방향 없는 그래프와 방향 있는 그래프
  • Unweighted / Weighted: 가중치 없는 그래프와 가중치 있는 그래프
  • Homogeneous / Heterogeneous: 동일 노드 구성 / 다양한 노드 구성
  • Labeled / Attributed: 노드나 엣지가 레이블 또는 속성을 가짐

---

2. 그래프 메트릭스

• Degree (차수)
  노드에 연결된 엣지의 수
  • IN Degree: 노드로 들어오는 엣지 수
  • OUT Degree: 노드에서 나가는 엣지 수
• Closeness Centrality (근접 중심성)
  노드와 다른 모든 노드 간의 최단 경로 길이의 역수로 정의:
  $C(v) = \frac{1}{\sum_{u \in V} d(v, u)}$
• Betweenness Centrality (중개 중심성)
  네트워크 내 최단 경로상에 등장하는 빈도수:
  $C_B(v) = \sum_{s \neq v \neq t} \frac{\sigma_{st}(v)}{\sigma_{st}}$
  • $\sigma_{st}$: $s$에서 $t$로 가는 최단 경로의 수
  • $\sigma_{st}(v)$: $v$를 포함하는 최단 경로의 수
• Eigenvector Centrality (중개 중심성)
  $X_i=\frac{1}{\lambda} \sum_{j \in N(i)} A_{ij} x_j$
• Flux-Capacity (플럭스 용량)
  IN Degree와 OUT Degree의 곱:
  $\text{Flux-Capacity} = \text{IN Degree} \times \text{OUT Degree}$

---

3. 그래프 수학적 표현

• Adjacency Matrix (인접 행렬)
  그래프를 행렬로 표현:
  $a_{ij} =
  \begin{cases}
  1, & \text{if } (i, j) \in E \
  0, & \text{otherwise}
  \end{cases}$
  • 무방향 그래프의 경우 $A$는 대칭 행렬
  • Weighted 그래프는 가중치 $w_{ij}$가 행렬 요소로 포함됨.
• Shortest Path (최단 경로)
  두 노드 간 경로 중 가장 짧은 경로:
  $d_{ij} = \min \sum_{(k,l) \in \text{Path}(i,j)} w_{kl}$

---

4. Evolving 랜덤(Erdős–Rényi) 그래프

• 정의
  랜덤 그래프는 확률 $p$로 엣지가 연결된 노드 쌍으로 구성:
  • 평균 차수: $\langle k \rangle = p \cdot (N-1)$
  • 포아송 분포: $P(k) = \frac{\lambda^k e^{-\lambda}}{k!}$
• 특징
  • 초기 상태: 트리 구조
  • 엣지 추가 시 "거대한 연결 성분"으로 전환 (Percolation Transition)

출처: Lecture2 slide p.45-46

---

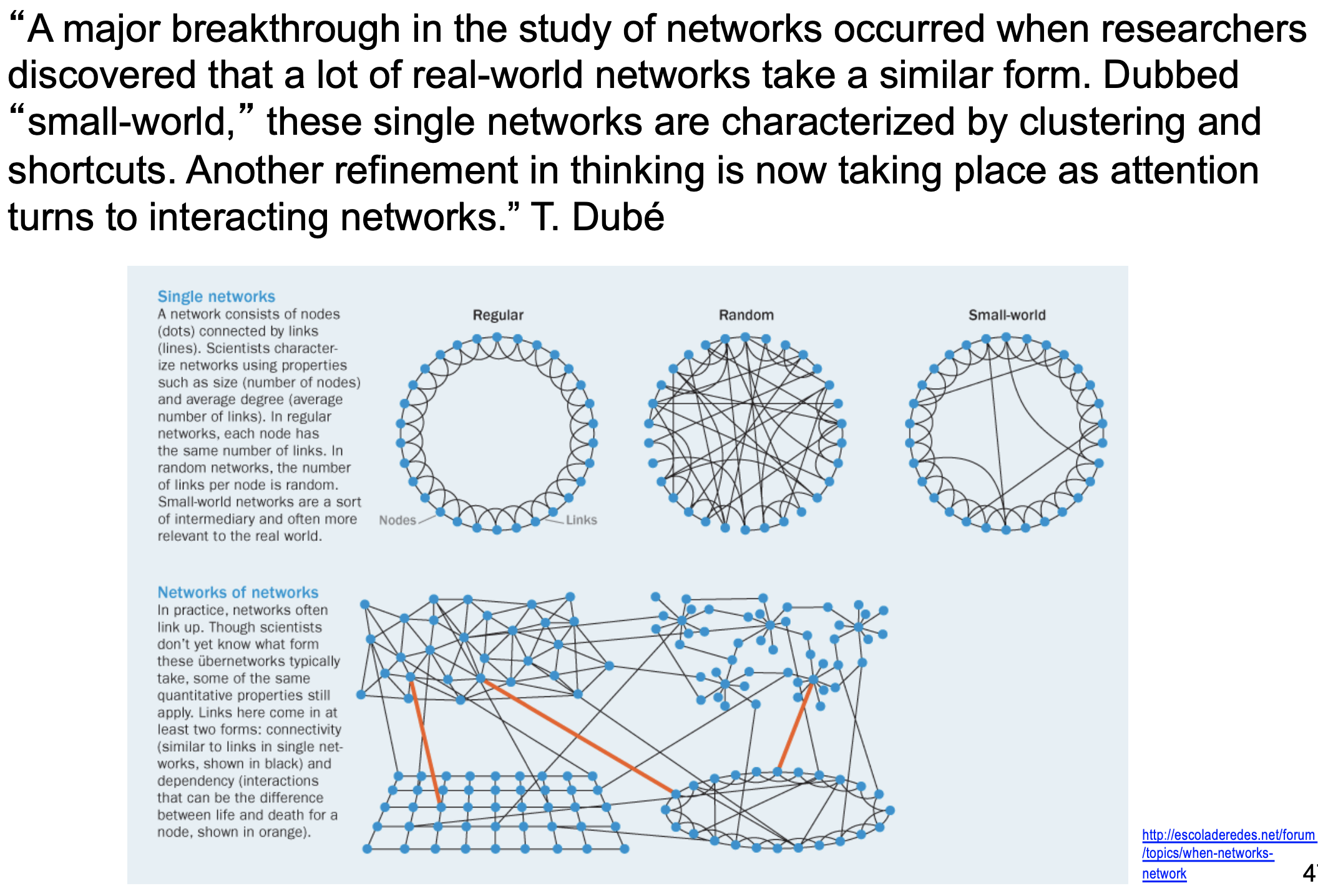
5. 스몰월드 네트워크 (SWN)

• 정의
  스몰월드 네트워크는 다음 두 가지 특징을 가짐:
  1. 높은 클러스터링 (Clustering Coefficient $C$)
  2. 짧은 평균 경로 길이 (Characteristic Path Length $L$)
• 메트릭
  • $C = \frac{\text{실제 엣지 수}}{\text{가능한 엣지 수}}$
  • $L = \frac{1}{|V|} \sum_{i,j \in V} d_{ij}$
• 응용
  • 신호 전파 속도 향상
  • 동기화 (Synchronizability) 개선
  • 감염병 및 소문 확산에 취약

---

6. 스케일 프리 네트워크 (SFN)

• 정의
  스케일 프리 네트워크는 멱법칙 분포를 따름:
  $P(k) \sim k^{-\gamma}$, $\gamma \approx 2-3$
• 특징
  • 우선 연결 (Preferential Attachment): 높은 차수를 가진 노드에 새 노드가 더 자주 연결됨.
  • Highly robust to random attacks/breakdowns, are Not robust to targeted attacks

---

7. 네트워크 과학의 응용

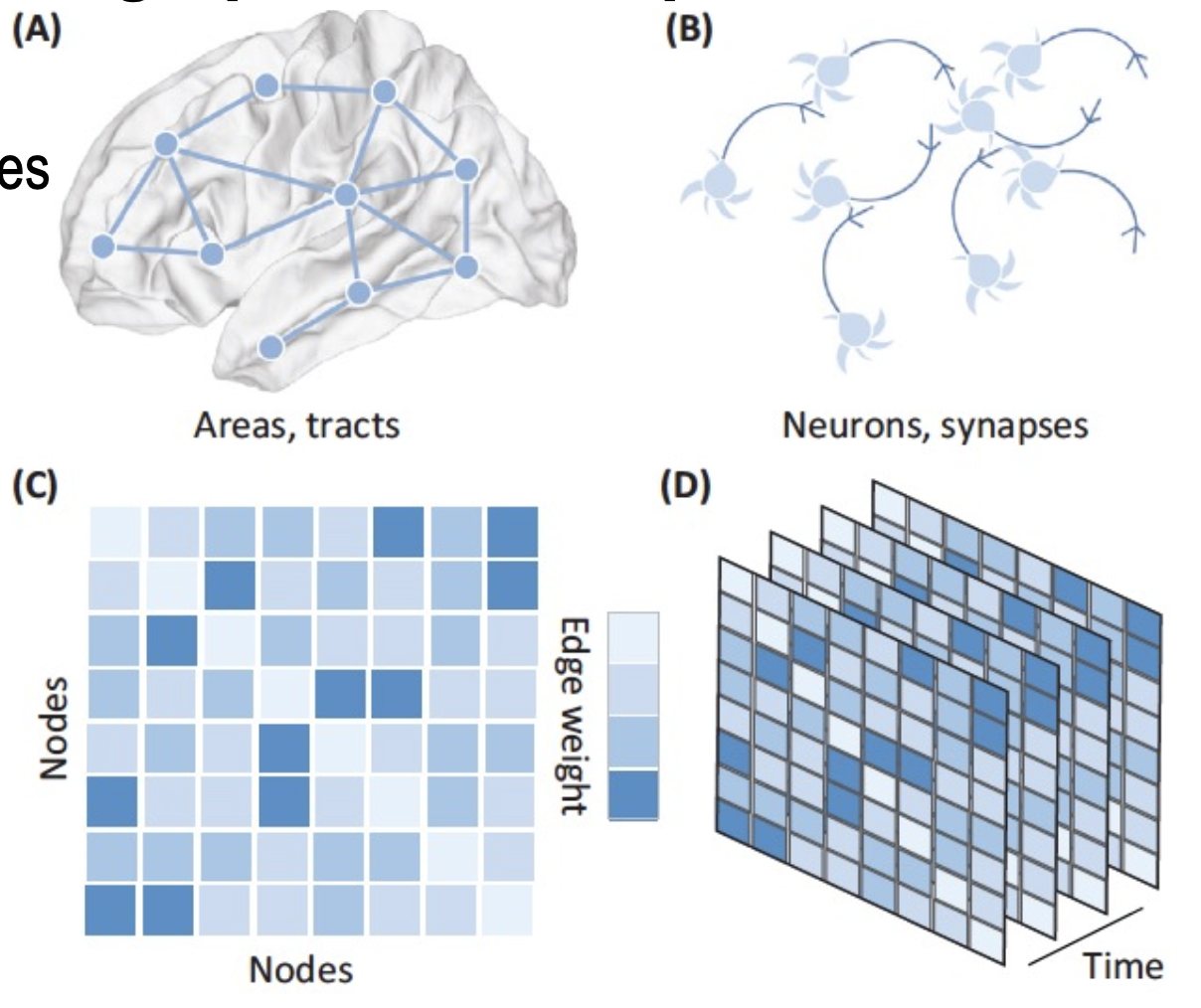
• 뇌 네트워크 분석
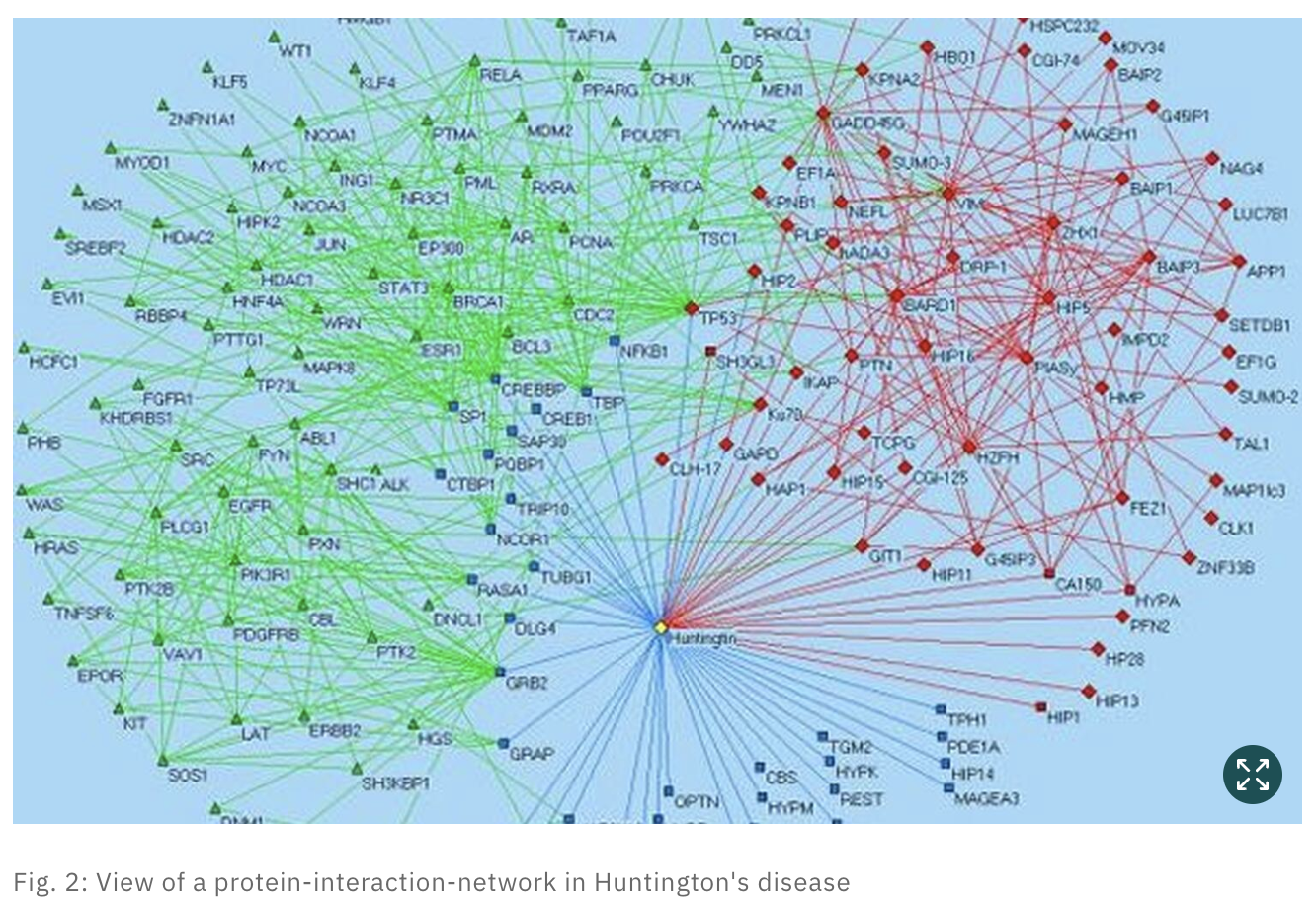
  뉴런 간 연결을 그래프로 표현하고, 학습 과정에서의 연결 변화 추적.
• 단백질-단백질 상호작용 네트워크 (PPIN)
  단백질 간 상호작용을 그래프로 모델링.
• 유전자 조절 네트워크 (GRN)
  유전자와 조절자의 관계를 나타내며, 바이파트 그래프로 모델

https://www.mdc-berlin.de/research/research_teams/proteomics_and_molecular_mechanisms_of_neurodegenerative_diseases/research/research1

https://www.ebi.ac.uk/training/online/courses/network-analysis-of-protein-interaction-data-an-introduction/protein-protein-interaction-networks/

---

8. 주요 그래프 모델 비교

• 랜덤 그래프 (ER)
  • 평균적인 구조와 포아송 분포.
• 스몰월드 네트워크 (SWN)
  • 짧은 경로 길이와 높은 클러스터링.
• 스케일 프리 네트워크 (SFN)
  • 멱법칙 분포, 우선 연결.