Lecture 5: Differential Geometry of Networks:
Ollivier-Ricci curvature, community detection, applications. Implications for automatic parallelization of software and hardware-soft-codesign, machine learning and artificial intelligence.
강의 개요
이번 강의는 네트워크의 기하학적 구조 분석을 위한 미분 기하학(Differential Geometry)와 Ollivier-Ricci Curvature (ORC)에 초점을 맞춘다.
ORC는 그래프의 곡률을 정의하여 네트워크 커뮤니티 탐지와 정보 전달 메커니즘을 이해하는 데 사용된다.
주요 내용은 다음과 같다:
1. 미분 기하학의 기초
- 곡률 (Curvature)
- 곡률은 기하학적 객체가 평평하지 않은 정도를 측정하는 지표이다.
- 곡선의 경우, 곡률은 다음과 같이 정의된다:
$ \text{Curvature} = \frac{1}{r}, \quad r = \text{Osculating Circle의 반지름} $ - 평면 곡선의 곡률은 점에서의 접촉 원을 기준으로 계산된다.
- 곡률이 양수일 경우 지오데식 경로가 수렴하며, 음수일 경우 발산한다.

- 다양체 (Manifold)
- 국소적으로 유클리드 공간처럼 보이는 위상 공간.
- 리만 다양체에서는 거리, 각도, 부피와 같은 기하학적 개념이 정의된다.

2. Ollivier-Ricci Curvature (ORC)
- ORC 정의
- 그래프 $ G = (V, E) $에서 각 노드 $ x $와 $ y $에 대해 중심 확률 분포 $ \mu_x, \mu_y $를 설정한다.
- ORC는 확률 분포 간의 Wasserstein 거리 $ W_1(\mu_x, \mu_y) $를 기반으로 정의된다:
$ \kappa(x, y) = 1 - \frac{W_1(\mu_x, \mu_y)}{d(x, y)} $
여기서 $ d(x, y) $는 그래프 상의 두 노드 사이의 거리이다.
- 특성
- $ \kappa(x, y) > 0 $: 고도로 연결된 노드 (클릭 구조).
- $ \kappa(x, y) < 0 $: 트리 구조 또는 네트워크의 다리 역할.
- $ \kappa(x, y) = 0 $: 평탄한 구조 (격자 네트워크).

3. ORC를 활용한 커뮤니티 탐지

- 커뮤니티의 정의
- 커뮤니티는 내부 연결 밀도가 높은 노드들의 하위 집합이다.
- 커뮤니티 내부 노드는 외부 노드보다 서로 강하게 연결된다.
- ORC 기반 커뮤니티 탐지
- 음의 곡률을 가지는 엣지를 제거하여 커뮤니티를 분리한다.
- 양의 곡률을 가지는 엣지는 강하게 연결된 구조를 형성한다.
- 최적의 모듈러리티를 달성하는 방법론:
$ Q = \frac{1}{2m} \sum_{ij} \left[ A_{ij} - \frac{k_i k_j}{2m} \right] \delta(c_i, c_j) $
여기서 $ A_{ij} $는 인접 행렬, $ k_i, k_j $는 노드의 차수, $ m $은 총 엣지 수, $ \delta $는 동일 커뮤니티 여부를 나타낸다.
4. Stochastic Block Model (SBM)
- SBM 정의
- 무작위 그래프 생성 모델로, 네트워크의 커뮤니티 구조를 모델링한다.
- 노드 간 엣지 존재 확률은 각 블록 간 확률 행렬 $ B $로 정의된다.
- SBM에서 ORC CI 성능
- 내부 커뮤니티 엣지 확률 $ p_{\text{in}} = 0.70 $, 외부 엣지 확률 $ p_{\text{out}} = 0.05 $일 때 높은 정확도를 보임.
- 커뮤니티 크기가 13개 이상의 노드로 구성될 경우 예측 정확도가 90%를 초과.
5. ORC의 실제 적용
- 사례 연구
- Zachary's Karate Club
- ORC는 기존 커뮤니티 외에도 추가 하위 구조를 발견.
- Zachary's Karate Club

- American Football Network
- ORC는 기존 알고리즘보다 정확히 커뮤니티를 탐지.

- Drug-Drug Interaction Network
- 약물-약물 상호작용 네트워크에서 ORC는 더 세밀한 하위 커뮤니티를 식별.
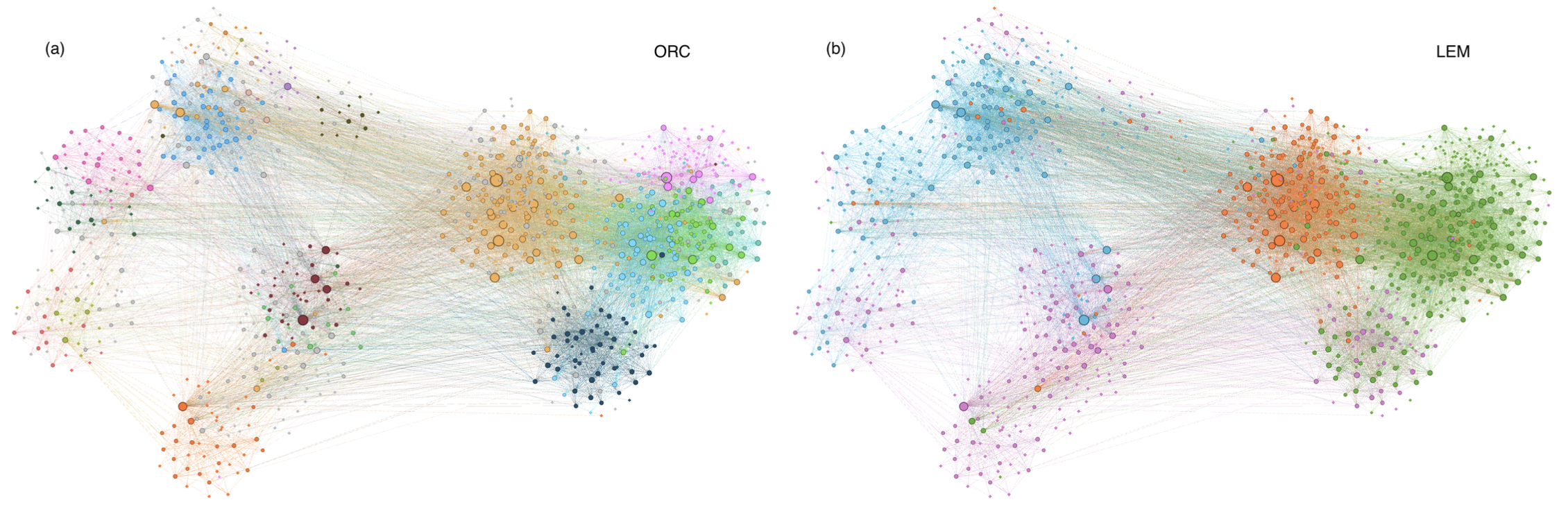
- 한계점
- 트리 형태의 네트워크에서는 음의 곡률 엣지가 다수 존재해 커뮤니티 과분할이 발생할 수 있음.
6. 추가 정보와 연구 방향
- ORC의 장점
- 네트워크의 구조적 특성과 위상적 정보를 결합하여 커뮤니티 구조를 탐지.
- 다양한 실제 네트워크에서 적용 가능.
- 향후 연구 방향
- 부분적으로 관측된 네트워크에 대해 ORC 기반 알고리즘 개선.
- 생물학적 데이터와 같은 외부 정보(Side Information)를 통합하여 성능 향상.
결론
Ollivier-Ricci Curvature는 그래프 곡률을 활용하여 네트워크의 복잡성을 정량화하고 커뮤니티 구조를 탐지하는 혁신적인 접근법이다.
강의에서는 이론적 기초와 실제 사례를 통해 ORC 기반 커뮤니티 탐지의 장점과 한계를 다루었다.
ORC는 네트워크 과학, 생물학, 그리고 머신러닝 응용에서 유망한 도구로 평가된다.