(Lecture 8) Graphon definitions & Multifractal graph generators

Lecture 8: Graphon definitions & Multifractal graph generators: definitions, mathematical properties, controlling multifractality of weighted graphs / networks. Case studies in living (biological) neuronal networks from neuronal cultures and brain, chromatin conformation, material sciences

---

강의 개요

이번 강의는 Graphons의 정의와 수학적 성질, 그리고 Multifractal Graph Generators의 개념과 응용을 다룬다.

특히, Graphons를 활용하여 대규모 네트워크를 모델링하는 방법과 이를 다양한 실제 사례에 적용하는 방식을 살펴본다.

(좌) Iñiguez, Gerardo, Federico Battiston, and Márton Karsai. "Bridging the gap between graphs and networks." Communications Physics 3, no. 1 (2020): 88. https://www.nature.com/articles/s42005-020-0359-6 , (우) Yin, Chenzhong, Xiongye Xiao, Valeriu Balaban, Mikhail E. Kandel, Young Jae Lee, Gabriel Popescu, and Paul Bogdan. "Network science characteristics of brain-derived neuronal cultures deciphered from quantitative phase imaging data." Scientific reports 10, no. 1 (2020): 15078. https://www.nature.com/articles/s41598-020-72013-7

 

---

1. Graphons: 정의와 개념

• Graphon의 직관적 정의
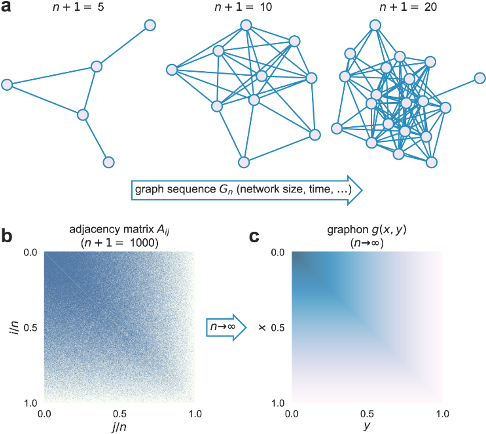
  Graphon은 유한 그래프의 시퀀스가 증가할 때, 그 한계를 함수로 표현한 것이다.
  주어진 그래프의 분포(예: Erdos-Renyi, Barabasi-Albert 모델)를 기반으로 정의되며, 단위 정사각형 상에서의 함수로 나타난다.

• Graphon의 수학적 정의
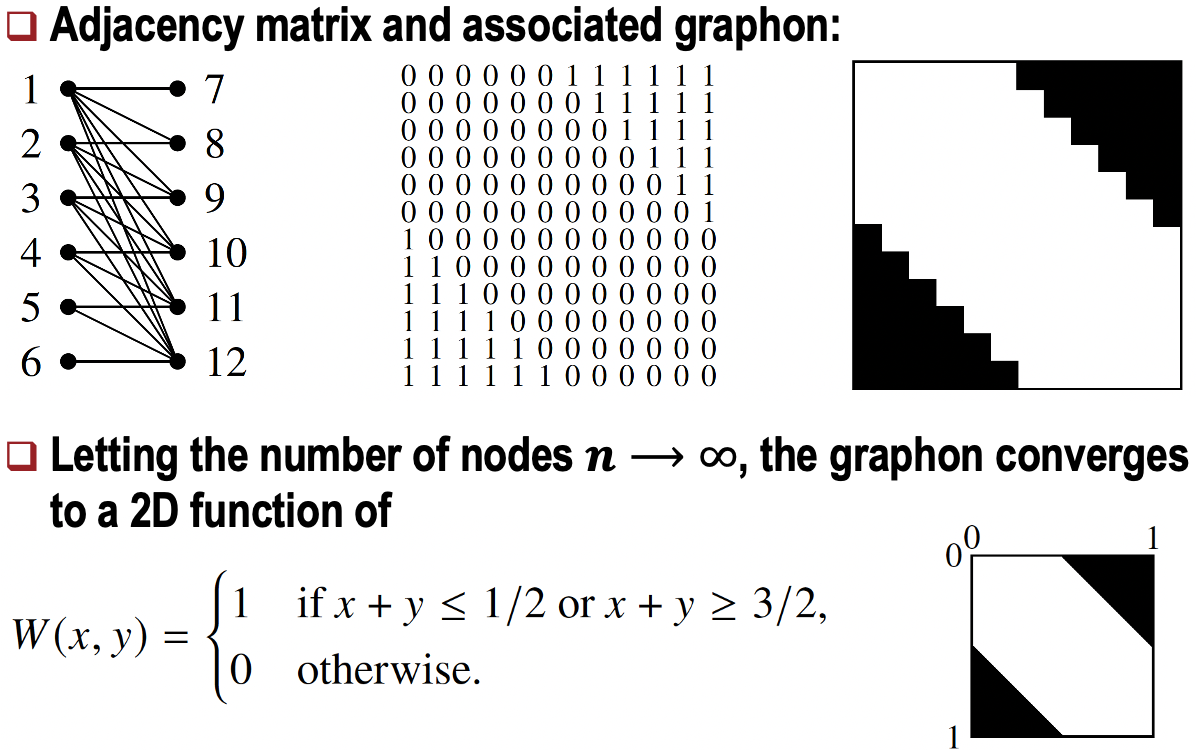
  Graphon은 대칭적인 함수 $W : [0,1]^2 \to [0,1]$로 정의된다.
  노드 $u, v$가 $[0,1]$에서 균등 분포로 샘플링될 때, 엣지 확률은 $W(u,v)$로 주어진다.
• 그래프 시퀀스와 Graphon의 관계
  무한 그래프 시퀀스 ${G_n}$의 한계로 Graphon이 나타난다.

• 대표적인 Graphon 모델
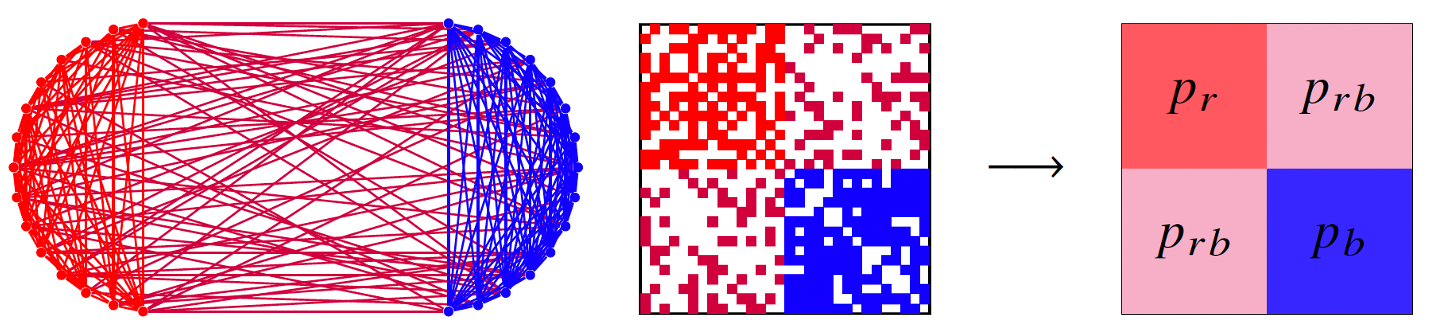
  • Stochastic Block Model (SBM): 노드 집합이 서로 다른 군집으로 나뉘며, 군집 간 엣지 확률이 다르게 설정된다.
  • Erdos-Renyi 그래프: 모든 노드 쌍 간 엣지 확률이 동일하다.

A red and a blue node are independently connected with probability p_rb

---

2. Graphons의 주요 수학적 개념

• Cut Distance
  두 Graphon $W$와 $W'$ 사이의 거리를 정의하는 개념으로, 다음과 같이 계산된다:
  $
  \delta_{\square}(W, W') = \inf_{\phi} \sup_{S, T \subseteq [0,1]} \left| \int_{S \times T} W(u,v) - W'(\phi(u),\phi(v)) ,du,dv \right|
  $
  여기서 $\phi$는 $[0,1]$ 위의 가측 재매핑이다.
• Homomorphism Density
  작은 그래프 $F$에서 큰 그래프 $G$로의 homomorphism 수를 나타낸다:
  $
  t(F, W) = \int_{[0,1]^{|V(F)|}} \prod_{(u,v) \in E(F)} W(x_u, x_v) \prod_{u \in V(F)} dx_u
  $
• Graphon 공간
  모든 Graphon은 특정 거리와 함수 공간의 구조 아래에서 하나의 공간으로 간주된다.

---

3. Multifractal Graph Generators

• Multifractal 그래프 생성 모델 정의
  Multifractal Graph Generator는 노드의 자기유사성을 기반으로 그래프를 생성한다.
  $q$차 모멘트를 기반으로 다음과 같은 특성을 정의한다:
  $
  M_q(l) = \sum_{i=1}^{N_l} \mu_i^q
  $

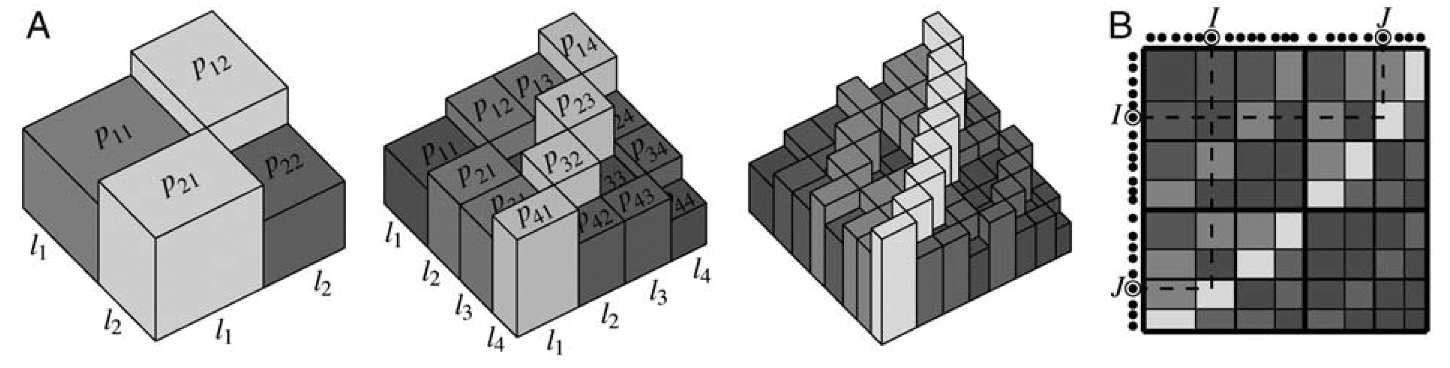
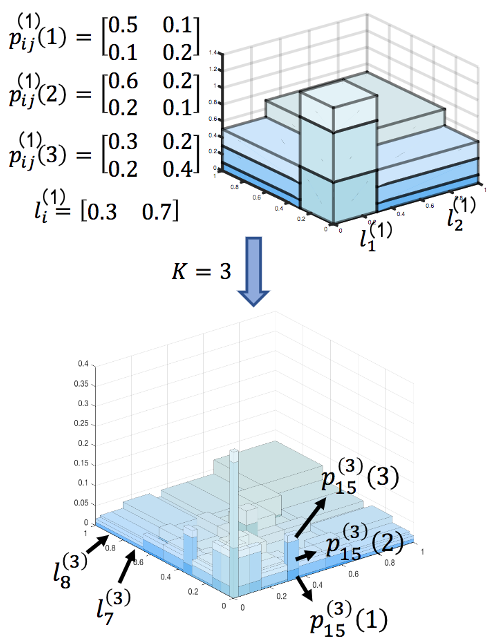
• Weighted Multifractal Graph (WMG) 모델
  노드 간 엣지 가중치를 다음과 같은 규칙으로 할당한다:
  $
  w(u, v) = P(u, v) \cdot f(u) \cdot f(v)
  $
  여기서 $P(u, v)$는 노드 쌍 간 연결 확률, $f(u)$는 노드 $u$의 가중치 함수다.

(좌) Palla, Gergely, László Lovász, and Tamás Vicsek. "Multifractal network generator." Proceedings of the National Academy of Sciences 107, no. 17 (2010): 7640-7645. , (우) Yang, Ruochen, and Paul Bogdan. "Controlling the multifractal generating measures of complex networks." Scientific reports 10, no. 1 (2020): 5541.

---

4. 사례 연구

• 뉴런 네트워크 분석
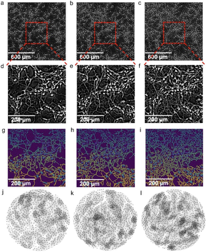
  뉴런 네트워크에서 Graphons와 Multifractal 분석을 사용하여 자기 최적화 및 네트워크 구조적 특징을 탐구.
  • 뉴런 간 연결은 자기유사적 구조를 가지며, 클러스터링 계수가 높게 나타남.
• 게놈 구조 분석
  Hi-C 데이터를 기반으로 유전자 구조의 3D 조직화를 Graphons로 모델링.
  특정 조건에서 유전자 간 상호작용 빈도를 최적화하는 방법 탐색.
• 알츠하이머 환자의 뇌 네트워크
  알츠하이머 환자와 정상인의 뇌 네트워크를 비교하여 Multifractal 특성 차이를 분석.

---

5. Graphons의 응용

• 대규모 네트워크 모델링
  적은 수의 매개변수로 대규모 네트워크의 구조를 설명.
• 동기화 분석
  커플링된 진동자의 네트워크 동기화 속도와 Graphons 간 상관관계 연구.
• 인공신경망의 안정성 평가
  Graphons를 사용해 GNN(Graph Neural Networks)의 견고성과 전이 가능성을 정량화.

---

결론

Graphons는 그래프의 극한 개념을 통해 대규모 네트워크를 효율적으로 모델링하고 분석하는 강력한 도구를 제공한다. Multifractal Graph Generators는 자기유사성과 네트워크의 다중 스케일 특성을 반영하여 복잡한 네트워크의 설계 및 분석에 활용될 수 있다.