728x90
Lecture 10: Fractional difference operators. Single variable autoregressive fractionally integrated moving average (ARFIMA) & multi-variate ARFIMA models. Applications to physiological processes, brain activity mining, and brain-machine interfaces

강의 개요
이 강의에서는 Fractional Calculus (FC)의 개념과 Fractional Difference Operators를 탐구하며,
ARFIMA (Autoregressive Fractionally Integrated Moving Average) 모델의 수학적 배경과 응용을 다룬다.
주요 응용 사례로는 생리학적 데이터, 뇌 활동 분석, 그리고 Brain-Machine Interface (BMI)가 포함된다.
1. Fractional Calculus (FC)
- Fractional Calculus 정의
Fractional Calculus는 비정수 차수의 적분 및 미분 연산을 다루며, 물리적 및 생물학적 시스템의 메모리와 장기 의존성을 모델링한다. - Fractional Order Differential Operator
$
D^q f(t) = \frac{1}{\Gamma(-q)} \int_0^t (t-\tau)^{-q-1} f(\tau) d\tau
$
여기서 $q$는 미분의 차수, $\Gamma$는 감마 함수이다. - 장점
- 비평탄적, 비미분 가능한 현상을 모델링할 수 있다.
- 시스템의 메모리 효과를 정량화한다.

2. Fractional Difference Operators
- 정의
Fractional Difference Operator는 Fractional Calculus를 차분 연산에 확장한 개념이다:
$
\Delta^d x_t = \sum_{k=0}^\infty \binom{d}{k} (-1)^k x_{t-k}
$
여기서 $d$는 차수, $\binom{d}{k}$는 이항 계수이다. - 응용
- 데이터의 장기 메모리와 의존성을 반영하여 예측 정확도를 개선한다.
- 기존 ARIMA 모델의 한계를 극복.

3. ARFIMA 모델

- ARFIMA 모델 정의
ARFIMA($p, d, q$)는 Fractional Difference Operators를 포함하는 확장된 ARIMA 모델이다:
$
\Phi(B)(1-B)^d x_t = \Theta(B)\epsilon_t
$- $\Phi(B)$: AR 다항식.
- $(1-B)^d$: Fractional Difference Operator.
- $\Theta(B)$: MA 다항식.
- $\epsilon_t$: 백색 잡음.
- 장점
- 장기 메모리를 가진 시계열 데이터에 적합.
- 자율 시스템 및 복잡한 네트워크 모델링에 효과적.
4. Fractional Calculus의 수학적 성질
- 스케일 불변성
Fractional Calculus는 다음 관계를 만족한다:
$
D^q \left[c \cdot f(t)\right] = c \cdot D^q f(t)
$- 이는 스케일 불변성을 갖는 동적 시스템을 설명하는 데 유용하다.
- Mittag-Leffler 함수
Fractional Differential Equation의 일반 해는 Mittag-Leffler 함수로 표현된다:
$
E_\alpha(t) = \sum_{k=0}^\infty \frac{t^k}{\Gamma(\alpha k + 1)}
$

5. ARFIMA의 실제 응용
- 생리학적 신호 분석
- 심박수 데이터에서 장기 메모리 효과를 탐지.
- 생리적 이상 상태를 조기에 발견.
- 뇌 활동 분석
- EEG 신호의 스펙트럼 분석을 통해 신경 활동의 자기유사성을 파악.
- 알츠하이머 환자와 정상인의 뇌 네트워크를 비교.
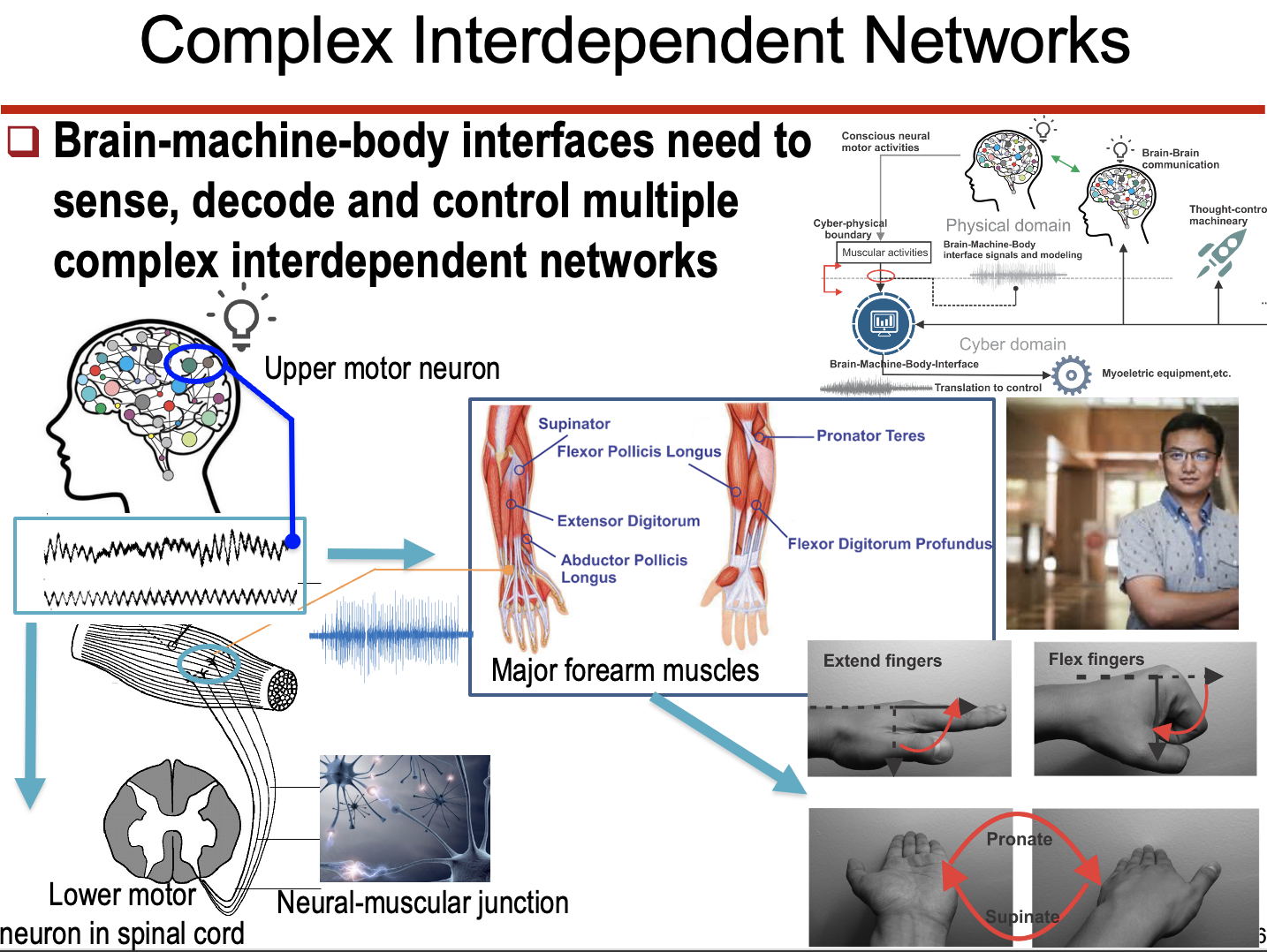
- Brain-Machine Interface (BMI)
- 신체-뇌 간 상호작용을 정량화하여 BMI의 효율성을 개선.
6. Fractional Difference Operators와 Hurst 지수
- Hurst 지수
Hurst 지수는 데이터의 장기 메모리를 측정한다:
$
H = \frac{1}{2} + d
$
여기서 $d$는 Fractional Difference Operator의 차수이다. - Hurst 지수 계산법
- R/S 분석.
- Detrended Fluctuation Analysis (DFA).
- Diffusion Entropy (DE).
결론
Fractional Calculus와 ARFIMA 모델은 복잡한 시계열 데이터와 장기 메모리를 가진 동적 시스템을 이해하고 분석하는 데 강력한 도구를 제공한다.
다양한 응용 사례에서 Fractional Difference Operators와 ARFIMA는 기존 모델보다 높은 성능을 입증했다.
728x90
반응형
'Learn > '24_Fall_(EE599) DataScience' 카테고리의 다른 글
| (Lecture 12) Structure and inference in hypergraphs with node attributes (1) | 2024.12.22 |
|---|---|
| (Lecture 11) ANNs, GNNs, RNNs, DNNs. (1) | 2024.12.22 |
| (Lecture 8) Graphon definitions & Multifractal graph generators (1) | 2024.12.22 |
| (Lecture 6) Detecting phase transition in time-varying weighted graphs from partial information (0) | 2024.12.22 |
| (Lecture 5) Differential geometry of networks (1) | 2024.12.21 |