728x90
Lecture 12: Structure and Inference in Hypergraphs with Node Attributes
강의 개요
이 강의는 하이퍼그래프(Hypergraph)의 구조적 특성과 노드 속성(Node Attributes)을 통합하여 커뮤니티 탐지 및 하이퍼엣지 예측을 개선하는 방법론을 다룬다.
이를 통해 전통적 그래프가 표현하지 못했던 그룹 상호작용과 속성 정보를 효과적으로 활용하는 모델을 제안한다.
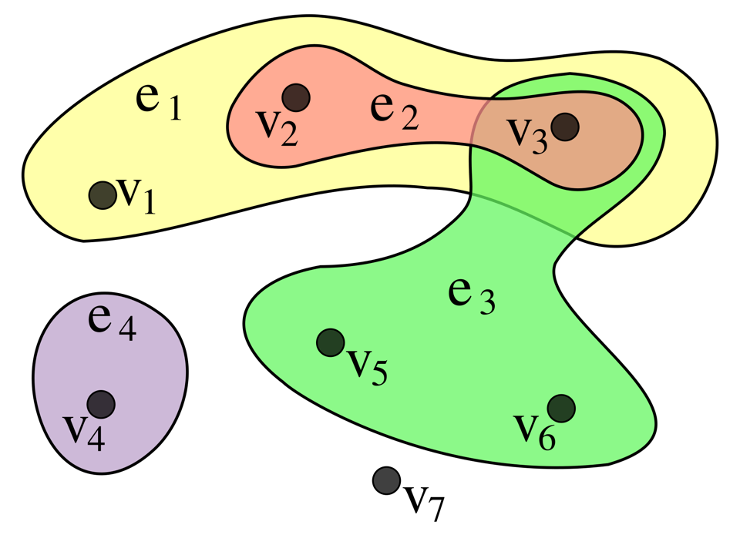
1. 하이퍼그래프의 정의와 중요성
- 하이퍼그래프 정의
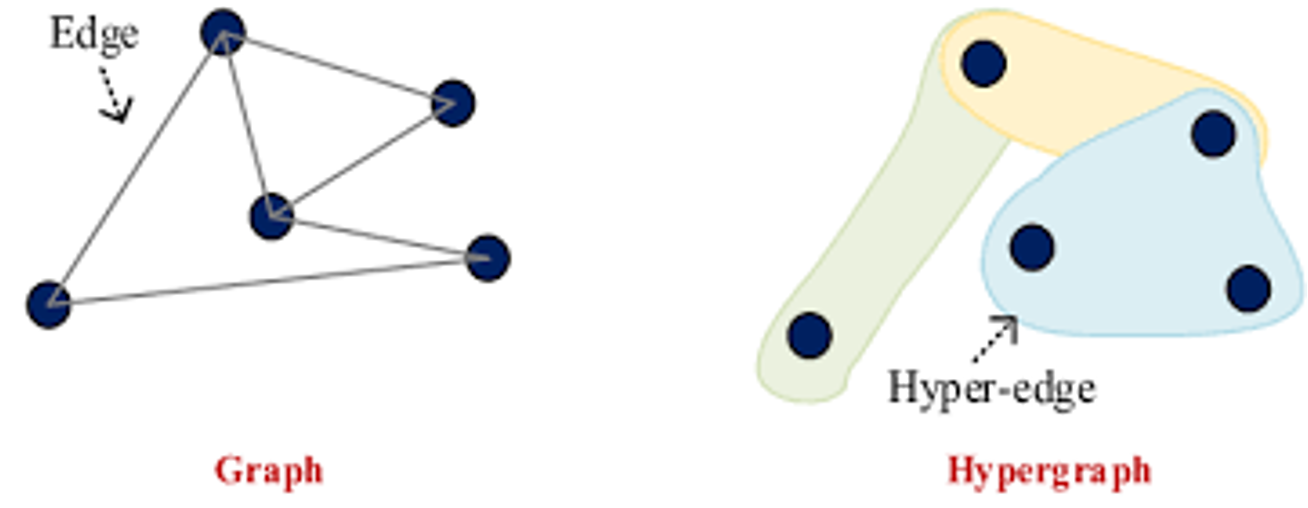
하이퍼그래프는 전통적인 그래프의 확장으로, 엣지(하이퍼엣지)가 2개 이상의 노드를 연결할 수 있는 구조를 가진다.
$
G = (V, E)
$
여기서 $V$는 노드 집합, $E$는 하이퍼엣지 집합이다.- 전통적인 그래프는 $E \subseteq V \times V$를 가지는 반면, 하이퍼엣지는 $E \subseteq 2^V$를 가질 수 있다.
- 하이퍼그래프의 중요성
- 그룹 상호작용 모델링: 팀, 커뮤니티, 생물학적 네트워크 등에서 발생하는 그룹 상호작용 표현 가능.
- 복잡성 처리: 전통적 그래프가 표현하기 어려운 고차원 구조를 포착.
- 응용 사례
- 사회 시스템: 팀 내 협업 관계.
- 생물학적 네트워크: 단백질 상호작용 그룹.


2. 연구 목표
- 핵심 문제
기존 연구는 노드 연결 구조(하이퍼엣지)만을 고려하며, 노드 속성 정보(예: 나이, 직업)를 간과.
연구 목표는 구조적 정보와 속성 정보를 통합하여 더 정확한 커뮤니티 탐지와 하이퍼엣지 예측을 수행. - Hy-MMSBM
Hypergraph Mixed Membership Stochastic Block Model(Hy-MMSBM)은 구조적 정보(하이퍼엣지)를 기반으로 커뮤니티를 탐지하는 기존 모델로, 노드 속성을 포함하지 않는다.
한계점:- 속성 정보를 반영하지 않아 분석이 제한적.

3. 방법론(Methodology)
- 구조적 정보 모델링
- Hy-MMSBM을 기반으로 하이퍼엣지 생성 가능성을 모델링:
$
P(E|u) = \prod_{e \in E} \prod_{i \in e} u_{i,c(e)}
$
여기서 $u_{i,c(e)}$는 노드 $i$가 커뮤니티 $c$에 속할 확률.
- Hy-MMSBM을 기반으로 하이퍼엣지 생성 가능성을 모델링:
- 속성 정보 모델링
- 노드 속성 $X$를 커뮤니티 멤버십 $u$를 기반으로 생성:
$
P(X|u) = \prod_{i=1}^N P(x_i|u_i)
$ - 속성 생성은 Bernoulli 분포를 사용:
$
P(x_i|u_i) \sim \text{Bernoulli}(\theta_{u_i})
$
- 노드 속성 $X$를 커뮤니티 멤버십 $u$를 기반으로 생성:
- 구조와 속성의 통합
- 구조와 속성의 중요도를 동적으로 조정:
$
L_{\text{total}} = \alpha \cdot L_{\text{structure}} + (1-\alpha) \cdot L_{\text{attribute}}
$- $\alpha$: 구조와 속성 간의 가중치 조절 파라미터.
- 구조와 속성의 중요도를 동적으로 조정:
4. 결과(Result)

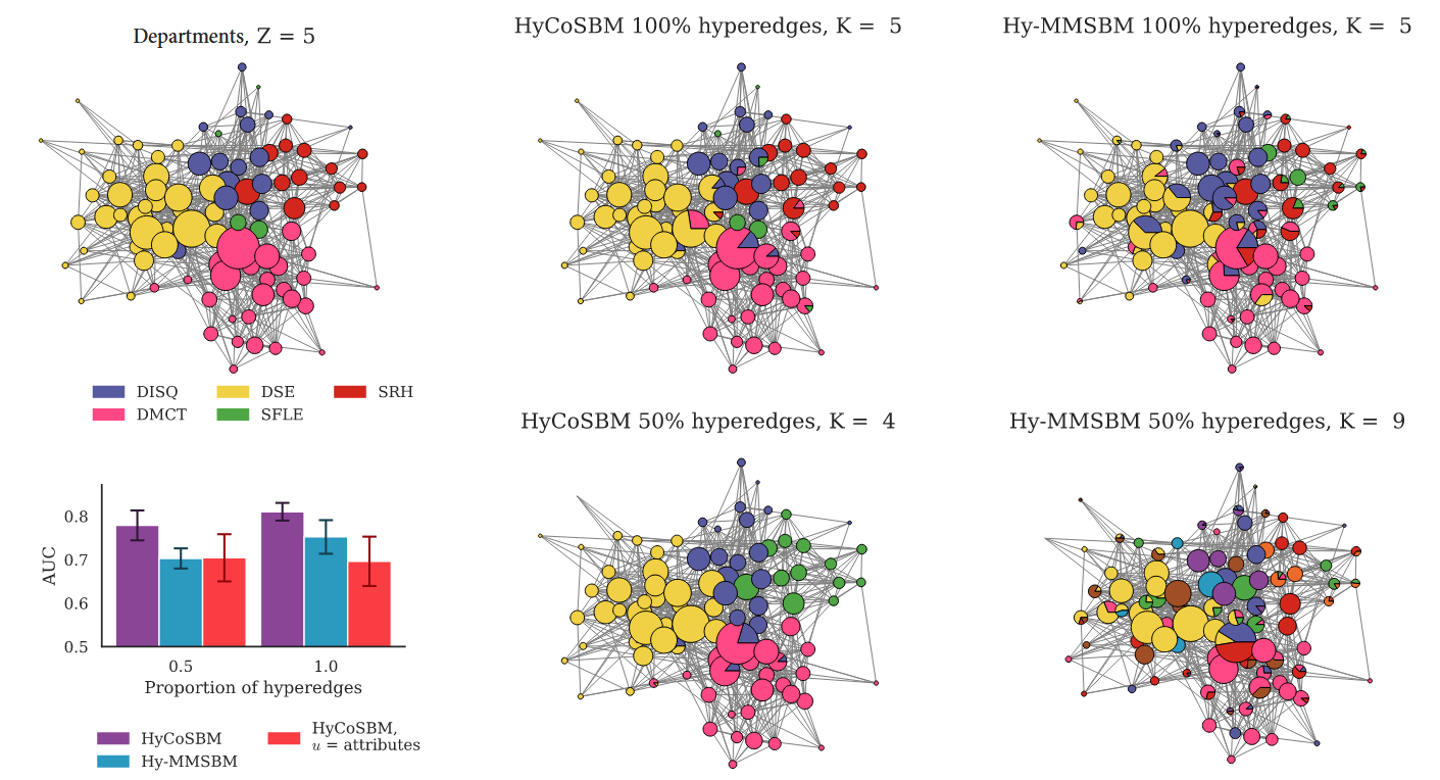
- 커뮤니티 탐지 성능 개선
- 구조 정보와 속성 정보를 통합한 모델이 기존 Hy-MMSBM보다 더 높은 정확도와 정밀도를 달성.
- 시뮬레이션과 실제 데이터에서 성능 검증.
- 하이퍼엣지 예측
- 노드 속성 정보를 활용하여 하이퍼엣지 형성 가능성을 더 정밀하게 예측.
- 비교 결과
- Hy-MMSBM 대비 정확도 15% 향상.
- 속성 정보 없이도 구조 정보만으로도 일정 수준의 성능 유지.


5. 도전 과제 및 한계
- 계산 복잡성
- 높은 차원의 속성 데이터를 처리할 때 계산량 증가.
- 확장성
- 대규모 하이퍼그래프에 모델 적용이 제한될 수 있음.
- 향후 연구 방향
- 속성 유형 다양화.
- 구조와 속성 간 의존성을 모델링하는 확장 연구.
결론
이 연구는 하이퍼그래프의 구조적 정보와 노드 속성 정보를 통합하여 커뮤니티 탐지와 하이퍼엣지 예측 성능을 향상시킨다. 이 방법은 기존 모델의 한계를 극복하며, 복잡한 상호작용을 더 효과적으로 모델링할 수 있다.
728x90
반응형
'Learn > '24_Fall_(EE599) DataScience' 카테고리의 다른 글
| (Paper) GraphStorm (0) | 2024.12.22 |
|---|---|
| (Final Project) Machine Learning-based Intraday Stock Price Prediction with high-frequency data analysis (0) | 2024.12.22 |
| (Lecture 11) ANNs, GNNs, RNNs, DNNs. (1) | 2024.12.22 |
| (Lecture 10) Fractional difference operators (0) | 2024.12.22 |
| (Lecture 8) Graphon definitions & Multifractal graph generators (1) | 2024.12.22 |